题目内容
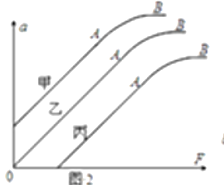
【题目】如图所示，在倾角为θ=30°的光滑斜面上有完全相同的质量为1kg的三个木块，A、B之间用轻弹簧相连，B、C之间用不可伸长的细绳相连，在手的恒定拉力F拉动下，达到稳定后，一起向上做匀加速运动，g大小取10m/s2 ， 下列说法正确的是（ ）
A.如果增大斜面的倾角，弹簧的弹力将增大
B.如果换成粗糙的斜面，弹簧的弹力和细绳的弹力将保持不变
C.如果一起运动加速度大小为5m/s2 ． 在突然撤去拉力F瞬间BC之间的弹力大小为5N
D.如果一起运动加速度大小为5m/s2在突然撤去拉力F瞬间 aA=5 m/s2 ， aB=aC=﹣10 m/s2（取沿斜面向上为正方向）
【答案】B,C,D
【解析】解：对整体受力分析，根据牛顿第二定律可知：F﹣3mgsinθ=3ma，解得：a= 
，此时对A受力分析可知：F弹﹣mgsinθ=ma，解得： 
A、如果增大斜面的倾角，弹簧的弹力 ，与角度无关，弹簧的弹力不变，A不符合题意；
B、如果换成粗糙的斜面，根据牛顿第二定律可知：F﹣3mgsinθ﹣3μmgcosθ=3ma，解得： 
= 
，对A可知：F弹﹣mgsinθ﹣μmgsinθ=ma，解得： ，以AB为整体有：F′弹﹣2mgsinθ﹣2μmgcos=2ma，解得： 
，与斜面的粗糙程度无关，B符合题意；
CD、对整体受力分析，根据牛顿第二定律可知F﹣3mgsinθ=3ma，解得F=30N，当撤去外力瞬间，AB间的弹力 
，对A： 
，解得：a=5m/s2
对BC组成的系统有： 
，解得：a′=10m/s2，对C：mgsinθ﹣F′=ma，解得：F′=5N，CD符合题意
所以答案是：BCD
【考点精析】掌握力的合成是解答本题的根本，需要知道求几个已知力的合力，叫做力的合成；共点的两个力（F 1 和F 2 ）合力大小F的取值范围为:|F 1 -F 2 |≤F≤F 1 +F 2．
