题目内容
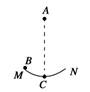
用图示装置来验证动量守恒定律.质量为mA的钢球A用细线悬挂于O点,质量为mB的钢球B放在离地面高为H的小支柱上,O点到小球A的距离为L,小球释放前悬线伸直且悬线与竖直方向的夹角为α.小球A释放后到最低点与B发生正碰,碰撞后,B做平抛运动,A小球把轻杆指针OC推移到与竖直方向成夹角γ的位置,在地面上铺一张带有复写纸的白纸D.保持α角度不变,多次重复,在白纸上记录了多个B球的落地点.
(1)图中的s应该是B球处位置到______的水平距离.
(2)为了验证两球碰撞过程中动量守恒,需要测______等物理量.
(3)用测得的物理量表示碰撞前后A球和B球的动量依次为PA=______,PB=______,PA′=______,PB′=______.

(1)图中的s应该是B球处位置到______的水平距离.
(2)为了验证两球碰撞过程中动量守恒,需要测______等物理量.
(3)用测得的物理量表示碰撞前后A球和B球的动量依次为PA=______,PB=______,PA′=______,PB′=______.

(1)图中的s应该是B球处位置到B球各次落地点所在最小圆的圆心的水平距离.
(2)小球从A处下摆过程只有重力做功,机械能守恒,由机械能守恒定律得:
mAgL(1-cosα)=
mAvA2-0,解得vA=
.则PA=mA
.
小球A与小球B碰撞后继续运动,在A碰后到达最左端过程中,机械能再次守恒,
由机械能守恒定律得:-mAgL(1-cosγ)=0-
mAvA′2,解得vA′=
,则PA′=mA
.
碰前小球B静止,则PB=0;
碰撞后B球做平抛运动,水平方向:S=vB′t,竖直方向H=
gt2,解得vB′=s
,则PB′=mBs
.
所以需要测量的物理量有mA mB L α γ s H.
故答案为:(1)B球各次落地点所在最小圆的圆心
(2)mAmBLαγsH
(3)mA
,0,mA
,mBs
.
(2)小球从A处下摆过程只有重力做功,机械能守恒,由机械能守恒定律得:
mAgL(1-cosα)=
| 1 |
| 2 |
| 2gL(1-cosα) |
| 2gL(1-cosα) |
小球A与小球B碰撞后继续运动,在A碰后到达最左端过程中,机械能再次守恒,
由机械能守恒定律得:-mAgL(1-cosγ)=0-
| 1 |
| 2 |
| 2gL(1-cosγ) |
| 2gL(1-cosγ) |
碰前小球B静止,则PB=0;
碰撞后B球做平抛运动,水平方向:S=vB′t,竖直方向H=
| 1 |
| 2 |
|
|
所以需要测量的物理量有mA mB L α γ s H.
故答案为:(1)B球各次落地点所在最小圆的圆心
(2)mAmBLαγsH
(3)mA
| 2gL(1-cosα) |
| 2gL(1-cosγ) |
|

练习册系列答案
相关题目


 飞行的子弹分别穿透两块由同种材料制成的固定木板,若子弹穿透木板后的速度分别是0.6
飞行的子弹分别穿透两块由同种材料制成的固定木板,若子弹穿透木板后的速度分别是0.6