Question

【题目】如图所示，半径R=0.5m的光滑绝缘圆形轨道固定在竖直面内，电荷量q=0．2C、质量m=0．2kg的带正电小球静止于轨道内侧最低点A，整个装置处于水平向右的匀强电场中，电场强度为E，现给小球水平向右的瞬时冲量I，已知重力加速度g取10m／s2。

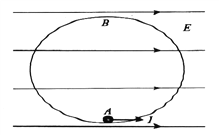
(1)通过计算说明，小球能否通过轨道最高点B与电场强度大小E是否有关，若小球能够通过最高点B，题干中所给物理量需要满足什么条件。

(2)若E=10N／C且小球恰好可沿轨道运动至B点，求运动过程中小球与轨道间弹力的最大值(结果可保留根号)。

(3)若保持水平冲量I及电场强度大小与(2)中相同，仅把电场强度的方向调整为竖直向下，求小球沿轨道上升的最大高度。

Answer 1

【答案】（1）小球能否通过轨道最高点B与电场强度大小E无关， （2） (3)

【解析】试题分析：(1)由题意小球恰好可运动到B点，小球与轨道间弹力为0，由牛顿第二定律求出小球在B点的速度，再小球由A点到B点过程由动能定理求出小球的初速度从而判断小球能否通过轨道最高点B与电场强度有无关系；

(2)利用“等效重力”找到“等效最低点即与轨道间作用力最大由动能定理求出此处的速度，再利用牛顿第二定律求出作用力 ；

(3)由动能定理和牛顿第二定律求出最大高度。

解：(1)小球恰好可运动到B点，小球与轨道间弹力为0，对小球由牛顿第二定律可得：，解得

对小球由A点到B点过程由动能定理得

解得

小球能否通过轨道最高点B与电场强度大小E无关，与A点的初速度有关，即与冲量I有关，；

(2)小球到达等效最低点时速度最大，与轨道间作用力最大，从A点到等效最低点由动能定理得

解得

对小球在等效最低点由牛顿第二定律得

解得： ；

(3)设小球在C点脱离轨道，C点与圆心连线与水平方向成角，由牛顿第二定律：

从最低点A到C点由动能定理得

解得：

由小球沿轨道运动的最大高度

解得：。

点晴：解决本题关键利用“等效重力场”找出最低点即速度最大（作用力）最大的位置，综合动能定理和牛顿第二定律求出。