题目内容
16.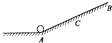 如图所示,小球从A点以初速度v0沿粗糙斜面向上运动,到达最高点B后返回A,C为AB的中点.下列说法中正确的是( )
如图所示,小球从A点以初速度v0沿粗糙斜面向上运动,到达最高点B后返回A,C为AB的中点.下列说法中正确的是( )| A. | 小球从A出发到返回A的过程中,位移为零,外力做功为零 | |
| B. | 小球从A到C与从C到B的过程,减少的动能相等 | |
| C. | 小球从A到C与从C到B的过程,速度的变化率相等 | |
| D. | 小球从A到C与从C到B的过程,损失的机械能不相等 |
分析 要求外力做功可以根据动能定理求;要求速度的变化量可以根据公式△v=a△t来求;而机械能的损失等于除重力外其他力所做的负功.
解答 解:A、位移是从初位置指向末位置的有向线段.故小球从A出发到返回A,位移为0.在整个过程中,摩擦力的方向与小球运动的方向始终相反,摩擦力对物体做负功,小球的机械能不断减小,返回A时速度小于出发时的速度,根据动能定理可知,外力做功不为零.故A错误.
B、设A到C的高度和从C到B的高度为h,AC的距离为s,斜面的倾角为θ,则有ssinθ=h
根据动能定理得:-mgh-μmgscosθs=△EK,可知小球从A到C过程中与从C到B过程合外力对物体做的功相同,故小球减少的动能相等.故B正确.
C、速度的变化率等于加速度,小球从A到C的合外力大小F1=mgsinθ+μmgcosθ,从C到B的合外力大小F2=mgsinθ+μmgcosθ,方向均沿斜面向下,根据牛顿第二定律可知,小球从A到C的加速度等于从C到B的加速度,则小球从A到C的速度的变化率等于从C到B的速度的变化率,故C正确.
D、克服除重力之外其它力做多少功物体的机械能就减少多少,根据μmgscosθ=△E可得小球从A到C过程与从C到B过程,损失的机械能相等.故D错误.
故选:BC.
点评 解决本题的关键是灵活运用动能定理和功能关系分析物体能量转化情况,知道外力做功与动能的变化有关,机械能的变化与克服除重力之外其它力做功有关.

练习册系列答案
 新课标同步训练系列答案
新课标同步训练系列答案 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案
相关题目
6.关于运动和力的关系,下列说法中不正确的是( )
| A. | 力是维持物体运动的原因 | B. | 力是使物体做变速运动的原因 | ||
| C. | 力能改变物体运动速度 | D. | 力是改变物体运动状态的原因 |
7.有一接地的导体球壳,如图所示,球心处放一点电荷q,达到静电平衡时,则( )


| A. | q的电量变化时,球壳外电场随之改变 | |
| B. | q在球壳外产生的电场强度为零 | |
| C. | 球壳内、外表面的电荷在壳外的合场强为零 | |
| D. | q与球壳内表面的电荷在壳外的合场强为零 |
11.关于运动和力的关系,下列说法中正确的是( )
| A. | 物体受到的合外力越大,加速度越大 | |
| B. | 物体受到的合外力越大,速度越大 | |
| C. | 物体从静止开始在外力作用下做直线运动,当合外力逐渐减小时,速度也逐渐减小 | |
| D. | 物体原来做匀变速直线运动,当合外力逐渐增大时,速度也一定逐渐增大 |
1.如图所示,先后以速度υ1和υ2匀速把一矩形线圈拉出有界匀强磁场区域,υ1=2υ2.在先后两种情况下( )
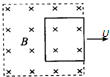

| A. | 线圈中的感应电流之比I1:I2=2:1 | |
| B. | 线圈中的感应电流之比I1:I2=1:2 | |
| C. | 线圈中产生的焦耳热之比Q1:Q2=4:1 | |
| D. | 通过线圈某截面的电荷量之比q1:q2=2:1 |
8. 如图所示,一根用绝缘材料制成的足够长轻质弹簧,弹簧一端固定,整个装置放在光滑的水平面上.开始时,弹簧处于原长状态且小球静止,小球带电量为-q,当加上水平向右的匀强电场E后,小球开始在水平面内做匀加速运动,当小球与弹簧接触后,下列说法中正确的是( )
如图所示,一根用绝缘材料制成的足够长轻质弹簧,弹簧一端固定,整个装置放在光滑的水平面上.开始时,弹簧处于原长状态且小球静止,小球带电量为-q,当加上水平向右的匀强电场E后,小球开始在水平面内做匀加速运动,当小球与弹簧接触后,下列说法中正确的是( )
 如图所示,一根用绝缘材料制成的足够长轻质弹簧,弹簧一端固定,整个装置放在光滑的水平面上.开始时,弹簧处于原长状态且小球静止,小球带电量为-q,当加上水平向右的匀强电场E后,小球开始在水平面内做匀加速运动,当小球与弹簧接触后,下列说法中正确的是( )
如图所示,一根用绝缘材料制成的足够长轻质弹簧,弹簧一端固定,整个装置放在光滑的水平面上.开始时,弹簧处于原长状态且小球静止,小球带电量为-q,当加上水平向右的匀强电场E后,小球开始在水平面内做匀加速运动,当小球与弹簧接触后,下列说法中正确的是( )| A. | 小球立即做减速运动 | |
| B. | 小球的速度增大时,弹簧的弹性势能可能减小 | |
| C. | 当弹簧的弹力等于电场力Eq时,小球静止 | |
| D. | 当弹簧压缩量最大时,小球的加速度为零 |
5.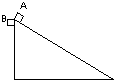 如图所示,质量相同的两物体处于同一高度,A沿固定在地面上的光滑斜面下滑,B自由下落,最后到达同一水平面,则( )
如图所示,质量相同的两物体处于同一高度,A沿固定在地面上的光滑斜面下滑,B自由下落,最后到达同一水平面,则( )
 如图所示,质量相同的两物体处于同一高度,A沿固定在地面上的光滑斜面下滑,B自由下落,最后到达同一水平面,则( )
如图所示,质量相同的两物体处于同一高度,A沿固定在地面上的光滑斜面下滑,B自由下落,最后到达同一水平面,则( )| A. | 重力对两物体做功相同 | |
| B. | 重力的平均功率相同 | |
| C. | 到达底端时重力的瞬时功率PA大于PB | |
| D. | 到达底端时两物体的速度相同 |