Question

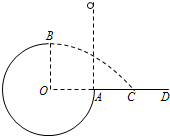（2010?上海二模）如图所示，竖直平面内的

3

4

圆弧形光滑轨道半径为R，A端与圆心O等高，AD为水平面，B点在O的正上方，一个小球在A点正上方由静止释放，自由下落至A点进入圆轨道并恰能到达B点．求：
（1）释放点距A点的竖直高度；
（2）落点C与A点的水平距离．

Answer 1

分析：（1）小球恰能到达B点，知小球到达B点时对轨道的压力为0，重力提供向心力，mg=m

vB2

R

求出B点的速度，从释放点到B点运用动能定理，根据动能定理求出释放点距离A点的高度．
（2）小球离开B点做平抛运动，高度决定时间，根据时间和B点的速度求出水平距离．

解答：解：（1）小球恰能到达B点，知小球到达B点时对轨道的压力为0，重力提供向心力，
mg=m

vB2

R

①
从释放点到B点运用动能定理得：
mg（h-R）=

1

2

mvB2②
由①②解得：h=

3

2

R
（2）小球离开B点做平抛运动，
根据R=

1

2

gt2
得：t=

2R g

所以落点C与A点的水平距离x=v_Bt=(

2

-1)R
答：（1）释放点距A点的竖直高度为

3

2

R；
（2）落点C与A点的水平距离为(

2

-1)R．

点评：解决本题的关键知道球到达C点时对轨道的压力为0，有mg=m

vB2

R

，以及能够熟练运用动能定理．