题目内容
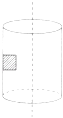
【题目】半径为R=0.9m的光滑半圆形轨道固定在水平地面上,与水平面相切于A点,在距离A点1.3m处有一可视为质点的小滑块,质量为m=0.5kg,小滑块与水平面间的动摩擦因数为μ=0.2,施加一个大小为F=11N的水平推力,运动到A点撤去推力,滑块从圆轨道最低点A处冲上竖直轨道.(g=10m/s2)问:
(1)滑块在B处对轨道的压力;
(2)滑块通过B点后的落地点到B点的水平距离.
【答案】
(1)解:从开始到B点的过程由动能定理得:
![]() mvB2﹣0=Fx﹣μmgx﹣mg2R
mvB2﹣0=Fx﹣μmgx﹣mg2R
代入数据解得:vB=4m/s
对滑块在B点受力分析,受重力和轨道对滑块的压力,由牛顿第二定律:
FN+mg=m ![]()
解得:FN=3.9N
根据牛顿第三定律知道轨道对小球的压力滑块在B处对轨道的压力大小相等,方向相反
所以滑块在B处对轨道的压力大小为3.9N,方向竖直向上
答:滑块在B处对轨道的压力大小为3.9N,方向竖直向上
(2)解:离开B点做平抛运动:z
竖直方向:2R= ![]() gt2
gt2
水平方向:x=vt
解得:x=2.4m
答:滑块通过B点后的落地点到B点的水平距离为2.4m
【解析】(1)先根据动能定理求出最高点时的速度,再结合向心力的公式,在最高点是合外力提供向心力列方程求解。
(2)与平抛运动的规律列方程求解。
【考点精析】通过灵活运用平抛运动和向心力,掌握特点:①具有水平方向的初速度;②只受重力作用,是加速度为重力加速度g的匀变速曲线运动;运动规律:平抛运动可以分解为水平方向的匀速直线运动和竖直方向的自由落体运动;向心力总是指向圆心,产生向心加速度,向心力只改变线速度的方向,不改变速度的大小;向心力是根据力的效果命名的.在分析做圆周运动的质点受力情况时,千万不可在物体受力之外再添加一个向心力即可以解答此题.

练习册系列答案
相关题目