题目内容
14.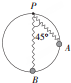 如图所示,劲度系数为k的轻质弹簧,一端系在竖直放置、半径为R的光滑圆环顶点P,另一端连接一套在圆环上且质量为m的小球.开始时小球位于A点,此时弹簧处于原长且与竖直方向的夹角为45°,之后小球由静止沿圆环下滑,小球运动到最低点B时的速率为v,此时小球与圆环之间的压力恰好为零,已知重力加速度为g,下列分析正确的是( )
如图所示,劲度系数为k的轻质弹簧,一端系在竖直放置、半径为R的光滑圆环顶点P,另一端连接一套在圆环上且质量为m的小球.开始时小球位于A点,此时弹簧处于原长且与竖直方向的夹角为45°,之后小球由静止沿圆环下滑,小球运动到最低点B时的速率为v,此时小球与圆环之间的压力恰好为零,已知重力加速度为g,下列分析正确的是( )| A. | 轻质弹簧的原长为R | |
| B. | 小球过B点时,弹簧的弹力为m$\frac{{v}^{2}}{R}$+mg | |
| C. | 小球从A到B的过程中,重力势能转化为弹簧的弹性势能和小球的动能 | |
| D. | 小球运动到B点时,弹簧的弹性势能为mgR-$\frac{1}{2}$mv2 |
分析 从A运动到B的过程中,小球的机械能减小.小球受到弹簧的弹力做负功,重力做正功,根据功能关系分析能量是如何转化的.小球过B点时,由重力和弹簧弹力的合力提供向心力,根据牛顿第二定律求出弹簧的弹力.
解答 解:A、由题意知,小球位于A点时弹簧处于原长,由几何知识可知弹簧的原长为 $\sqrt{2}$R,故A错误;
B、小球过B点时,由重力和弹簧弹力的合力提供小球的向心力,根据向心力公式:F-mg=m$\frac{{v}^{2}}{R}$,则得弹簧的弹力F=m$\frac{{v}^{2}}{R}$+mg,故B正确;
C、以小球和弹簧组成的系统为研究对象,在小球从A到B的过程中,只有重力和弹簧的弹力做功,系统的机械能守恒,小球重力势能减小转化为弹簧的弹性势能和小球的动能.故C正确.
D、根据能量的转化与守恒:mgR=$\frac{1}{2}$mv2+EP 得:弹簧的弹性势能为 EP=mgR-$\frac{1}{2}$mv2,故D正确;
故选:BCD.
点评 此题中小球的机械能不守恒,可以从能量转化的角度进行分析.小球过B点时,弹簧的弹力不是合力,不能得到这样的表达式:F=m$\frac{{v}^{2}}{R}$.

练习册系列答案
 优生乐园系列答案
优生乐园系列答案 新编小学单元自测题系列答案
新编小学单元自测题系列答案
相关题目
5. 空间某区域竖直平面内存在电场,电场线分布如图所示.一个质量为m、电量为q,电性未知的小球在该电场中运动,小球经过A点时的速度大小为v1,方向水平向右,运动至B点的速度大小为v2.若A、B两点之间的高度差为h,则以下判断中正确的是( )
空间某区域竖直平面内存在电场,电场线分布如图所示.一个质量为m、电量为q,电性未知的小球在该电场中运动,小球经过A点时的速度大小为v1,方向水平向右,运动至B点的速度大小为v2.若A、B两点之间的高度差为h,则以下判断中正确的是( )
 空间某区域竖直平面内存在电场,电场线分布如图所示.一个质量为m、电量为q,电性未知的小球在该电场中运动,小球经过A点时的速度大小为v1,方向水平向右,运动至B点的速度大小为v2.若A、B两点之间的高度差为h,则以下判断中正确的是( )
空间某区域竖直平面内存在电场,电场线分布如图所示.一个质量为m、电量为q,电性未知的小球在该电场中运动,小球经过A点时的速度大小为v1,方向水平向右,运动至B点的速度大小为v2.若A、B两点之间的高度差为h,则以下判断中正确的是( )| A. | A、B两点的电场强度和电势大小关系为EA<EB、φA<φB | |
| B. | 若v2>v1,则电场力一定做正功 | |
| C. | 若小球带正电,则A、B两点间的电势差为$\frac{m}{2q}$(v22-v12-2gh) | |
| D. | 小球从A运动到B点的过程中电场力做的功为$\frac{1}{2}$mv22-$\frac{1}{2}$mv12 |
2. 超导电磁船是一种不需要螺旋桨推进的低噪音新型船,如图是电磁船的简化原理图,MN和CD是与电池相连的导体棒,MN与CD之间部分区域有垂直纸面向内的匀强磁场(磁场由超导线圈产生,其独立电路部分未画出),以下说法正确的是( )
超导电磁船是一种不需要螺旋桨推进的低噪音新型船,如图是电磁船的简化原理图,MN和CD是与电池相连的导体棒,MN与CD之间部分区域有垂直纸面向内的匀强磁场(磁场由超导线圈产生,其独立电路部分未画出),以下说法正确的是( )
 超导电磁船是一种不需要螺旋桨推进的低噪音新型船,如图是电磁船的简化原理图,MN和CD是与电池相连的导体棒,MN与CD之间部分区域有垂直纸面向内的匀强磁场(磁场由超导线圈产生,其独立电路部分未画出),以下说法正确的是( )
超导电磁船是一种不需要螺旋桨推进的低噪音新型船,如图是电磁船的简化原理图,MN和CD是与电池相连的导体棒,MN与CD之间部分区域有垂直纸面向内的匀强磁场(磁场由超导线圈产生,其独立电路部分未画出),以下说法正确的是( )| A. | 要使船前进,图中MN导体棒应接直流电源的负极 | |
| B. | 改变超导线圈中电流的方向,可控制船前进或倒退 | |
| C. | 若接入电路的海水电阻为R,其两端的电压为U,电路中的电流为I,则UI>I2R | |
| D. | 该超导电磁船应用的是电磁感应原理 |
19.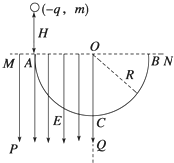 如图所示,ACB为光滑固定的半圆形轨道,轨道半径为R,A、B为圆水平直径的两个端点,AC为$\frac{1}{4}$圆弧,MPQO为有界的竖直向下的匀强电场,电场强度的大小E=$\frac{2mg}{q}$.一个质量为m,电荷量为-q的带电小球,从A点正上方高为H处由静止释放,并从A点沿切线进入半圆轨道.小球运动过程中电量不变,不计空气阻力及一切能量损失,已知重力加速度为g,关于带电小球的运动情况,下列说法正确的是( )
如图所示,ACB为光滑固定的半圆形轨道,轨道半径为R,A、B为圆水平直径的两个端点,AC为$\frac{1}{4}$圆弧,MPQO为有界的竖直向下的匀强电场,电场强度的大小E=$\frac{2mg}{q}$.一个质量为m,电荷量为-q的带电小球,从A点正上方高为H处由静止释放,并从A点沿切线进入半圆轨道.小球运动过程中电量不变,不计空气阻力及一切能量损失,已知重力加速度为g,关于带电小球的运动情况,下列说法正确的是( )
 如图所示,ACB为光滑固定的半圆形轨道,轨道半径为R,A、B为圆水平直径的两个端点,AC为$\frac{1}{4}$圆弧,MPQO为有界的竖直向下的匀强电场,电场强度的大小E=$\frac{2mg}{q}$.一个质量为m,电荷量为-q的带电小球,从A点正上方高为H处由静止释放,并从A点沿切线进入半圆轨道.小球运动过程中电量不变,不计空气阻力及一切能量损失,已知重力加速度为g,关于带电小球的运动情况,下列说法正确的是( )
如图所示,ACB为光滑固定的半圆形轨道,轨道半径为R,A、B为圆水平直径的两个端点,AC为$\frac{1}{4}$圆弧,MPQO为有界的竖直向下的匀强电场,电场强度的大小E=$\frac{2mg}{q}$.一个质量为m,电荷量为-q的带电小球,从A点正上方高为H处由静止释放,并从A点沿切线进入半圆轨道.小球运动过程中电量不变,不计空气阻力及一切能量损失,已知重力加速度为g,关于带电小球的运动情况,下列说法正确的是( )| A. | 若H=R,则小球到达C点的速度为零 | B. | 若H=2R,则小球到达B点的速度为零 | ||
| C. | 若H=3R,则小球到达C点的速度$\sqrt{2gR}$ | D. | 若 H=4R,则小球到达B点的速度$\sqrt{2gR}$ |
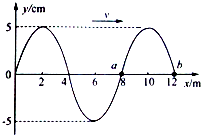 某介质中,x=0处的质点在t=0时刻开始振动,产生的波沿x轴正方向传播,t=0.3 s时刻,波的图象如图所示.质点b刚好开始振动.则此时质点a的振动方向为沿y轴负方向(填“正”或“负”),波在介质中传播的速度为40m/s.
某介质中,x=0处的质点在t=0时刻开始振动,产生的波沿x轴正方向传播,t=0.3 s时刻,波的图象如图所示.质点b刚好开始振动.则此时质点a的振动方向为沿y轴负方向(填“正”或“负”),波在介质中传播的速度为40m/s.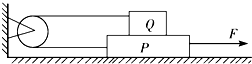 如图所示,位于水平桌面上的物块P,由跨过定滑轮的轻绳与物块相连,从滑轮到P和到Q的两段绳都是水平的,已知Q与P之间以及桌面之间的动摩擦因数都是μ,两物块的质量都是m,滑轮轴上的摩擦不计,若用一水平向右的力F拉P使其做匀速运动,则F的大小为( )
如图所示,位于水平桌面上的物块P,由跨过定滑轮的轻绳与物块相连,从滑轮到P和到Q的两段绳都是水平的,已知Q与P之间以及桌面之间的动摩擦因数都是μ,两物块的质量都是m,滑轮轴上的摩擦不计,若用一水平向右的力F拉P使其做匀速运动,则F的大小为( )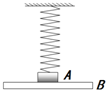 轻质弹簧上端固定,下端连接质量m=3kg的物块A,物块A放在平台B上,通过平台B可以控制A的运动,如图所示.初始时A、B静止,弹簧处于原长.已知弹簧的劲度系数k=200N/m,g=10m/s2.(计算结果保留两位有效数字)
轻质弹簧上端固定,下端连接质量m=3kg的物块A,物块A放在平台B上,通过平台B可以控制A的运动,如图所示.初始时A、B静止,弹簧处于原长.已知弹簧的劲度系数k=200N/m,g=10m/s2.(计算结果保留两位有效数字)