Question

【题目】如图所示，将一轻质弹簧放置在光滑的水平地面上，一端固定在竖直墙壁上的A点，另一端与质量m＝2kg的物块P（可视为质点）接触但不固定；半径R＝0.5m的光滑半圆轨道BCD和地面在B点相切，直径BD竖直．现用外力缓慢推动物块P，将弹簧压缩至O点由静止释放，物块P恰好能通过半圆轨道最高点D．重力加速度g＝10m/s2，空气阻力不计．则

⑴弹簧被压缩至O点时所具有的弹性势能Ep；

⑵物块P运动到圆轨道最低点B时，物块P对轨道的压力FB；

⑶若半圆轨道半径R可以改变，物块仍从O点静止释放，且要求物块运动到半圆最高点时对轨道的压力FN不超过400N，请推导FN与R关系式，并作出FN－的关系图象．

Answer 1

【答案】（1）25J （2）120N （3）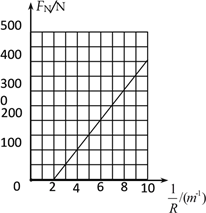

【解析】（1）小球在最高点有mg=m

根据能量守恒定律得： Ep=2mgR+mv2

Ep=25J

（2）Ep=mvB2

Fmg= m

根据牛顿第三定律得：FB= F=120N

（3）Ep=mvD2+2mgR

FN+mg= m

FN = 100（N）

0≤FN≤400N 0.1m≤ R ≤ 0.5m

图像如图；