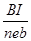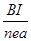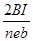题目内容
(9分) 如图所示,在倾角为30°的斜面OA的左侧有一竖直档板,其上有一小孔P,OP=0.5m.现有一质量m=4×10-20kg、电荷量q=+2×10-14C的粒子,从小孔以速度v0=3×104m/s水平射向磁感应强度B=0.2T、方向垂直纸面向外的圆形磁场区域,且在飞出磁场区域后能垂直打在OA面上,粒子重力不计.求:

(1)粒子在磁场中做圆周运动的半径;
(2)粒子在磁场中运动的时间;
(3)圆形磁场区域的最小半径.

(1)粒子在磁场中做圆周运动的半径;
(2)粒子在磁场中运动的时间;
(3)圆形磁场区域的最小半径.
(1)0.3m (2) (3)0.15m
(3)0.15m
 (3)0.15m
(3)0.15m试题分析:(1)带电粒子在磁场中做匀速圆周运动,洛伦兹力提供向心力
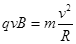
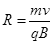 (2分)
(2分)解得 R=0.3m (1分)
(2)带电粒子进磁场的初速度方向水平向右,离开磁场的末速度垂直AO斜向下,速度偏向角为
 ,所以匀速圆周运动的圆心角也为60°,运动的时间为T/6,
,所以匀速圆周运动的圆心角也为60°,运动的时间为T/6,又
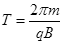 ,粒子在磁场中运动的时间为
,粒子在磁场中运动的时间为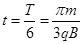 (2分)
(2分)解得
 (1分)
(1分)(3)根据粒子做匀速圆周运动圆心角为60°,可求得对应圆弧的弦长为R,最小的圆形区域即以该弦长作为直径,所以圆形磁场区域的最小半径rmin=
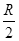 =0.15m (3分)
=0.15m (3分)
练习册系列答案
 捷径训练检测卷系列答案
捷径训练检测卷系列答案 小夫子全能检测系列答案
小夫子全能检测系列答案
相关题目










 =2∶1
=2∶1