题目内容
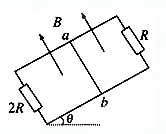
(10分)如图两根正对的平行金属直轨道MN、M´N´位于同一水平面上,两轨道间距L=0.50m.轨道的MM′端之间接一阻值R=0.40Ω的定值电阻,NN′端与两条位于竖直面内的半圆形光滑金属轨道NP、N′P′平滑连接,两半圆轨道的半径均为 R0 =0.50m.直轨道的右端处于竖直向下、磁感应强度B =0.64T的匀强磁场中,磁场区域的宽度d=0.80m,且其右边界与NN′重合.现有一质量 m =0.20kg、电阻 r =0.10Ω的导体杆ab静止在距磁场的左边界s=2.0m处.在与杆垂直的水平恒力 F =2.0N的作用下ab杆开始运动,当运动至磁场的左边界时撤去F,结果导体ab恰好能以最小速度通过半圆形轨道的最高点PP′.已知导体杆ab在运动过程中与轨道接触良好,且始终与轨道垂直,导体杆ab与直轨道间的动摩擦因数 μ=0.10,轨道的电阻可忽略不计,取g=10m/s2,求:

①导体杆穿过磁场的过程中通过电阻R上的电荷量
②导体杆穿过磁场的过程中整个电路产生的焦耳热

①导体杆穿过磁场的过程中通过电阻R上的电荷量
②导体杆穿过磁场的过程中整个电路产生的焦耳热
①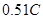 ②
②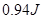
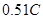 ②
②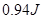
试题分析:①设导体杆在磁场中运动的时间为 t,由法拉第电磁感应定律得:
产生的感应电动势的平均值为
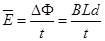
由闭合电路欧姆定律得:通过电阻 R 的感应电流的平均值为
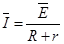
通过电阻R的电荷量
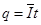
联立以上各式解得:
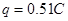 .
.②设导体杆在 F 的作用下运动到磁场的左边界时的速度为v1,导体杆离开磁场时的速度大小为v2,运动到圆轨道最高点的速度为v3,根据动能定理则有
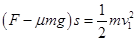 ,解得:
,解得: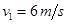
因导体杆恰好能以最小速度通过半圆形轨道的最高点,根据牛顿第二定律,对导体杆在轨道最高点时有
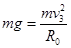
对于导体杆从NN′运动至 PP′的过程,根据机械能守恒定律有
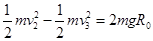
联立以上两式解得
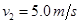
导体杆穿过磁场的过程中损失的机械能
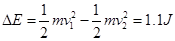
导体杆穿过磁场的过程,整个电路中机械能转化为内能,根据能量守恒定律
此过程,电路中产生的焦耳热为
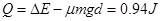 .
.
练习册系列答案
 新课标快乐提优暑假作业陕西旅游出版社系列答案
新课标快乐提优暑假作业陕西旅游出版社系列答案 暑假衔接培优教材浙江工商大学出版社系列答案
暑假衔接培优教材浙江工商大学出版社系列答案 欣语文化快乐暑假沈阳出版社系列答案
欣语文化快乐暑假沈阳出版社系列答案
相关题目

 ”形导轨PONQ,其质量为M=2.0kg,放在光滑绝缘的水平面上,处于匀强磁场中,另有一根质量为m=0.60kg的金属棒CD跨放在导轨上,CD与导轨的动摩擦因数是0.20,CD棒与ON边平行,左边靠着光滑的固定立柱a、b,匀强磁场以ab为界,左侧的磁场方向竖直向上(图中表示为垂直于纸面向外),右侧磁场方向水平向右,磁感应强度的大小都是0.80T,如图所示,已知导轨ON段长为0.50m,电阻是0.40Ω,金属棒CD的电阻是0.20Ω,其余电阻不计。导轨在水平拉力作用下由静止开始以0.20m/s2的加速度做匀加速直线运动,一直到CD中的电流达到4.0A时,导轨改做匀速直线运动.设导轨足够长,取g=10m/s2.求:
”形导轨PONQ,其质量为M=2.0kg,放在光滑绝缘的水平面上,处于匀强磁场中,另有一根质量为m=0.60kg的金属棒CD跨放在导轨上,CD与导轨的动摩擦因数是0.20,CD棒与ON边平行,左边靠着光滑的固定立柱a、b,匀强磁场以ab为界,左侧的磁场方向竖直向上(图中表示为垂直于纸面向外),右侧磁场方向水平向右,磁感应强度的大小都是0.80T,如图所示,已知导轨ON段长为0.50m,电阻是0.40Ω,金属棒CD的电阻是0.20Ω,其余电阻不计。导轨在水平拉力作用下由静止开始以0.20m/s2的加速度做匀加速直线运动,一直到CD中的电流达到4.0A时,导轨改做匀速直线运动.设导轨足够长,取g=10m/s2.求:
 平面第一象限整个区域分布匀强电场,电场方向平行
平面第一象限整个区域分布匀强电场,电场方向平行 轴向下,在第四象限内存在有界匀强磁场,左边界为
轴向下,在第四象限内存在有界匀强磁场,左边界为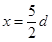 的直线,磁场方向垂直纸面向外。质量为
的直线,磁场方向垂直纸面向外。质量为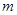 、带电量为
、带电量为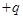 的粒子从
的粒子从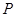 点以初速度
点以初速度 垂直
垂直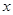 轴上
轴上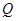 点以与
点以与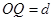 ,不计粒子重力。求:
,不计粒子重力。求: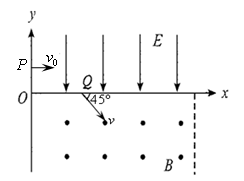
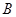 的取值范围;
的取值范围;