题目内容
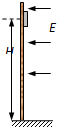
如图所示,离地H高处有一个质量为m、带电量为+q的物体处于电场强度随时间变化规律为E=E
0-kt(E
0、k均为大于零的常数,电场水平向左为正方向)的电场中,物体与竖直绝缘墙壁间的动摩擦因数为μ,已知μqE
0>mg.t=0时,物体从墙上静止释放,若物体所受的最大静摩擦力等于滑动摩擦力,当物体下滑
后脱离墙面,此时速度大小为
,最终落在地面上.则下列关于物体的运动说法正确的是( )
| A、当物体沿墙壁下滑时,物体先加速再做匀速直线运动 |
| B、物体从脱离墙壁到落地之前的运动轨迹是一段直线 |
| C、物体克服摩擦力所做的功W=mgH |
| D、物体与墙壁脱离的时刻为t= |
分析:分析物体的受力情况,根据牛顿第二定律通过加速度的变化判断物体的运动规律,根据合力与速度的方向确定物体的运动轨迹.根据动能定理,抓住电场力在沿墙面下滑的过程中不做功,求出物体克服摩擦力做功的大小,抓住电场强度的变化规律,结合电场力为零时,物体脱离墙面求出运动的时间.
解答:解:A、竖直方向上,由牛顿第二定律有:mg-μqE=ma,随着电场强度E的减小,加速度a逐渐增大,做变加速运动,当E=0时,加速度增大到重力加速度g,此后物块脱离墙面,故A错误.
B、物体脱离墙面时的速度向下,之后所受合外力与初速度不在同一条直线上,所以运动轨迹为曲线.故B错误.
C、物体从开始运动到脱离墙面电场力一直不做功,由动能定理得:mg
-W=
m()2,
物体克服摩擦力所做的功为:W=
mgH.故C正确.
B、当物体所受的墙面的支持力为零,则电场力为零,则此时电场强度为零,所以有:E=E
0-kt=0,
解得时间为:t=
.故D错误.
故选:CD.
点评:本题关键能运用牛顿第二定律,正确分析物体的运动情况,结合动能定理求解摩擦力做功,并要知道物体做直线运动还是曲线运动的条件.
练习册系列答案
相关题目
 如图所示,离地H高处有一个质量为m、带电量为+q的物体处于电场强度随时间变化规律为E=E0-kt(E0、k均为大于零的常数,电场水平向左为正方向)的电场中,物体与竖直绝缘墙壁间的动摩擦因数为μ,已知μqE0>mg.t=0时,物体从墙上静止释放,若物体所受的最大静摩擦力等于滑动摩擦力,当物体下滑
如图所示,离地H高处有一个质量为m、带电量为+q的物体处于电场强度随时间变化规律为E=E0-kt(E0、k均为大于零的常数,电场水平向左为正方向)的电场中,物体与竖直绝缘墙壁间的动摩擦因数为μ,已知μqE0>mg.t=0时,物体从墙上静止释放,若物体所受的最大静摩擦力等于滑动摩擦力,当物体下滑
 一本好题口算题卡系列答案
一本好题口算题卡系列答案 如图所示,离地H高处有一个质量为m、带电量为+q的物体处于电场强度随时间变化规律为E=E0-kt(E0、k均为大于零的常数,电场水平向左为正方向)的电场中,物体与竖直绝缘墙壁间的动摩擦因数为μ,已知μqE0>mg.t=0时,物体从墙上静止释放,若物体所受的最大静摩擦力等于滑动摩擦力,当物体下滑
如图所示,离地H高处有一个质量为m、带电量为+q的物体处于电场强度随时间变化规律为E=E0-kt(E0、k均为大于零的常数,电场水平向左为正方向)的电场中,物体与竖直绝缘墙壁间的动摩擦因数为μ,已知μqE0>mg.t=0时,物体从墙上静止释放,若物体所受的最大静摩擦力等于滑动摩擦力,当物体下滑 如图所示,离地H高处有一个质量为m、带电量为+q的物体处于电场强度随时间变化规律为E=E0-kt(E0、k均为大于零的常数,电场水平向左为正方向)的电场中,物体与竖直绝缘墙壁间的动摩擦因数为μ,已知μqE0>mg.t=0时,物体从墙上静止释放,若物体所受的最大静摩擦力等于滑动摩擦力,当物体下滑
如图所示,离地H高处有一个质量为m、带电量为+q的物体处于电场强度随时间变化规律为E=E0-kt(E0、k均为大于零的常数,电场水平向左为正方向)的电场中,物体与竖直绝缘墙壁间的动摩擦因数为μ,已知μqE0>mg.t=0时,物体从墙上静止释放,若物体所受的最大静摩擦力等于滑动摩擦力,当物体下滑 后脱离墙面,此时速度大小为
后脱离墙面,此时速度大小为 ,最终落在地面。
,最终落在地面。
 (
( 、
、 均为大于零的常数,电场水平向左为正方向)的电场中,物体与竖直绝缘墙壁间的动摩擦因数为
均为大于零的常数,电场水平向左为正方向)的电场中,物体与竖直绝缘墙壁间的动摩擦因数为 ,已知
,已知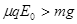 。
。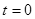 时,物体从墙上静止释放,若物体所受的最大静摩擦力等于滑动摩擦力,当物体下滑
时,物体从墙上静止释放,若物体所受的最大静摩擦力等于滑动摩擦力,当物体下滑 后脱离墙面,此时速度大小为
后脱离墙面,此时速度大小为 ,最终落在地面上。则下列关于物体的运动说法正确的是:
,最终落在地面上。则下列关于物体的运动说法正确的是:

