题目内容
2.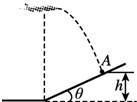 玩具轰炸机沿水平方向匀速飞行,到达山坡底端正上方时释放一颗炸弹,并垂直击中山坡上的目标A.已知A点高度为h=3.6m,山坡倾角为37°,g=10m/s2由此算出( )
玩具轰炸机沿水平方向匀速飞行,到达山坡底端正上方时释放一颗炸弹,并垂直击中山坡上的目标A.已知A点高度为h=3.6m,山坡倾角为37°,g=10m/s2由此算出( )| A. | 轰炸机的飞行高度为320m | |
| B. | 轰炸机的飞行速度8m/s | |
| C. | 炸弹的飞行时间0.8s | |
| D. | 炸弹落在上坡时的动能是炸弹投出时的动能的$\frac{5}{4}$倍 |
分析 因为平抛运动速度与水平方向夹角的正切值是位移与水平方向夹角正切值的2倍,速度方向的夹角得知位移与水平方向夹角的正切值,再通过水平位移求出竖直位移,从而得知轰炸机的飞行高度,炸弹的飞行时间,以及炸弹的初速度.
解答 解:A、B、C、设轰炸机的飞行高度为H,炸弹的飞行时间为t,初速度为v0.
炸弹的水平位移为:x=v0t=$\frac{h}{tanθ}$=$\frac{3.6}{0.75}=4.8$m
据题:炸弹垂直击中山坡上的目标A,则根据速度的分解有:tanθ=$\frac{{v}_{0}}{{v}_{y}}$=$\frac{{v}_{0}}{gt}$
又 $\frac{H-h}{x}$=$\frac{\frac{1}{2}g{t}^{2}}{{v}_{0}t}$=$\frac{gt}{2{v}_{0}}$
联立以上三式得:H=h+$\frac{h}{2ta{n}^{2}θ}$=3.6+$\frac{3.6}{2×(tan37°)^{2}}$=6.8m.
炸弹的飞行时间 t=$\sqrt{\frac{2(H-h)}{g}}$,可以求出t=0.8s.
轰炸机的飞行速度等于炸弹平抛运动的初速度,为 v0=$\frac{x}{t}$,可以求出v0=6m/s.故AB错误,C正确.
D、设炸弹的质量为m,则开始时:${E}_{K0}=\frac{1}{2}m{v}_{0}^{2}=\frac{1}{2}m×{6}^{2}=18m$
落地时:${E}_{K}=\frac{1}{2}m(\sqrt{{v}_{0}^{2}+(gt)^{2}})^{2}$=$\frac{1}{2}m×({v}_{0}^{2}+{g}^{2}{t}^{2})=\frac{1}{2}m×({6}^{2}+1{0}^{2}×0.{8}^{2})$=50m
炸弹落在上坡时的动能是炸弹投出时的动能的$\frac{50}{18}$倍.故D错误.
故选:C.
点评 解决本题的关键掌握平抛运动水平方向和竖直方向上的运动规律,知道平抛运动的一些推论,并能灵活运用.

| A. | 库仑 | B. | 牛顿 | C. | 富兰克林 | D. | 奥斯特 |

| A. | 电场强度 | B. | 电势差 | C. | 电势能 | D. | 电量 |
 如图所示,光滑绝缘细杆竖直放置,它与以正点电荷Q为圆心的某一圆周交于B、C点,质量为m,带电量为-q的有孔小球从杆上A点无初速下滑,已知q<<Q,AB=h,小球滑到B点时速度大小为$\sqrt{3gh}$.求:
如图所示,光滑绝缘细杆竖直放置,它与以正点电荷Q为圆心的某一圆周交于B、C点,质量为m,带电量为-q的有孔小球从杆上A点无初速下滑,已知q<<Q,AB=h,小球滑到B点时速度大小为$\sqrt{3gh}$.求: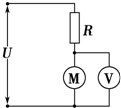 如图所示是一提升重物用的直流电动机工作时的电路图.电动机内电阻r=1Ω,电路中另一电阻R=10Ω,直流电压U=210V,电压表示数UV=110V.(g取10m/s2)试求:
如图所示是一提升重物用的直流电动机工作时的电路图.电动机内电阻r=1Ω,电路中另一电阻R=10Ω,直流电压U=210V,电压表示数UV=110V.(g取10m/s2)试求: