题目内容
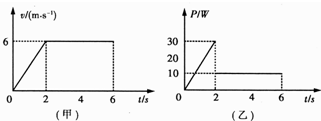
 (2009?咸宁模拟)如图所示,在以O为圆心,半径为R=10
(2009?咸宁模拟)如图所示,在以O为圆心,半径为R=10| 3 |
(1)求如果粒子垂直打在荧光屏上的P点,电压表的示数多大?
(2)调节滑动变阻器滑片P的位置,求粒子到打到光屏的范围.
分析:(1)粒子垂直打在荧光屏上的P点时,在磁场中运动轨迹必定为四分之一圆弧,由几何关系得其运动半径为R,由洛伦兹力提供向心力,可得运动速度,对于加速过程,由动能定理可得加速电压,此即两板间的电压
(2)滑动片在最左端时,有欧姆定律可解得结果,极板间电压最小,在最右端时电压最大,电压的变化会引起加速后速度达到变化,进而影响圆周运动的半径变化,故射出磁场时的偏角改变,射出磁场后粒子做匀速直线运动,可得粒子到打到光屏的范围.
(2)滑动片在最左端时,有欧姆定律可解得结果,极板间电压最小,在最右端时电压最大,电压的变化会引起加速后速度达到变化,进而影响圆周运动的半径变化,故射出磁场时的偏角改变,射出磁场后粒子做匀速直线运动,可得粒子到打到光屏的范围.
解答:解:(1)设离子由电场射出后进入磁场时的速度为v.因离子是沿圆心O的方向射入磁场,由对称性可知,离子射出磁场时的速度方向的反向延长线也必过圆心O.离开磁场后,离子垂直打在荧光屏上(图中的O′点),则离子在磁场中速度方向偏转了90°,由几何知识可知,离子在磁场中做圆周运动的半径
r′=R=10
cm①
设离子的电荷量为q、质量为m,进入磁场时的速度为v有
由qvB=m
得
r′=
②
设两金属板间的电压为U,离子在电场中加速,由动能定理有:
qU=
mv2③
而
=2×105C/kg ④
由②③两式可得
U=
⑤
代入有关数值可得U=30V,也就是电压表示数为30V.
(2)当滑动变阻器滑动头在左端时,由欧姆定律得:
U1=
R1=
×10v=10V,
qU1=
r1=
解得:r1=10cm,粒子进入磁场后的轨迹为图甲
由几何关系得偏转角为θ1=120°,故α=60°,
打在荧光屏上的M点,MO′=
=30cm
当滑动头在有端时,由欧姆定律得:
U2=
(R1+R2)=90V
qU2=
r2=
解得r2=30cm,粒子进入磁场后的轨迹为图乙,由几何关系得,
偏转角θ2=60°,故β=60°,打在荧光屏上的N点,且:
OO′N=
=30cm
故,调节滑动变阻器滑片P的位置,粒子到打到光屏的范围为60cm
答:(1)粒子垂直打在荧光屏上的P点,电压表的示数为30V
(2)粒子到打到光屏的范围为60cm
r′=R=10
| 3 |
设离子的电荷量为q、质量为m,进入磁场时的速度为v有
由qvB=m
| ||
| r′ |
r′=
| mv |
| qB |
设两金属板间的电压为U,离子在电场中加速,由动能定理有:
qU=
| 1 |
| 2 |
而
| q |
| m |
由②③两式可得
U=
| B2r′2q |
| 2m |
代入有关数值可得U=30V,也就是电压表示数为30V.
(2)当滑动变阻器滑动头在左端时,由欧姆定律得:

U1=
| E |
| R1+R2+r |
| 91 |
| 10+80+1 |
qU1=
| 1 |
| 2 |
| mv | 2 1 |
r1=
| mv1 |
| qB |
解得:r1=10cm,粒子进入磁场后的轨迹为图甲
由几何关系得偏转角为θ1=120°,故α=60°,
打在荧光屏上的M点,MO′=
| H | ||
|
当滑动头在有端时,由欧姆定律得:
U2=
| E |
| R1+R2+r |
qU2=
| 1 |
| 2 |
| mv | 2 2 |
r2=
| mv2 |
| qB |
解得r2=30cm,粒子进入磁场后的轨迹为图乙,由几何关系得,
偏转角θ2=60°,故β=60°,打在荧光屏上的N点,且:
OO′N=
| H | ||
|
故,调节滑动变阻器滑片P的位置,粒子到打到光屏的范围为60cm
答:(1)粒子垂直打在荧光屏上的P点,电压表的示数为30V
(2)粒子到打到光屏的范围为60cm
点评:本题分析离子的运动情况是求解的关键和基础,考查综合应用电路、磁场和几何知识,处理带电粒子在复合场中运动问题的能力,综合性较强.

练习册系列答案
相关题目

 (2009?咸宁模拟)如图所示,晾晒衣服的绳子两端分别固定在两根竖直杆上的A、B两点,绳子的质量及绳与衣架挂钩间摩擦均忽略不计,衣服处于静止状态.如果保持绳子A端、B端在杆上位置不变,将右侧杆平移到虚线位置,稳定后衣服仍处于静止状态.则( )
(2009?咸宁模拟)如图所示,晾晒衣服的绳子两端分别固定在两根竖直杆上的A、B两点,绳子的质量及绳与衣架挂钩间摩擦均忽略不计,衣服处于静止状态.如果保持绳子A端、B端在杆上位置不变,将右侧杆平移到虚线位置,稳定后衣服仍处于静止状态.则( )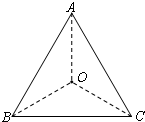 (2009?咸宁模拟)如图所示,一粒子源位于一边长为a的正三角形ABC的中点O处,可以在三角形所在的平面内向各个方向发射出速度大小为v、质量为m、电荷量为q的带电粒子,整个三角形位于垂直于△ABC的匀强磁场中,若使任意方向射出的带电粒子均不能射出三角形区域,则磁感应强度的最小值为( )
(2009?咸宁模拟)如图所示,一粒子源位于一边长为a的正三角形ABC的中点O处,可以在三角形所在的平面内向各个方向发射出速度大小为v、质量为m、电荷量为q的带电粒子,整个三角形位于垂直于△ABC的匀强磁场中,若使任意方向射出的带电粒子均不能射出三角形区域,则磁感应强度的最小值为( )