题目内容
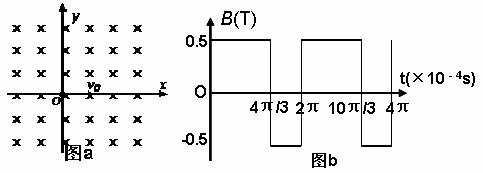
如图a所示的平面坐标系xOy,在整个区域内充满了匀强磁场,磁场方向垂直坐标平面,磁感应强度B随时间变化的关系如图b所示,开始时刻,磁场方向垂直纸面向内(如图).t=0时刻,有一带正电的粒子(不计重力)从坐标原点O沿x轴正向进入磁场,初速度为v0=2×103m/s.已知正粒子的比荷为1.0×104C/kg,其它有关数据见图中标示.试求:
(1)t=×10-4s时刻,粒子的坐标.
(2)粒子从开始时刻起经多长时间到达y轴.
(3)粒子是否还可以返回原点?如果可以,则经多长时间返回原点?
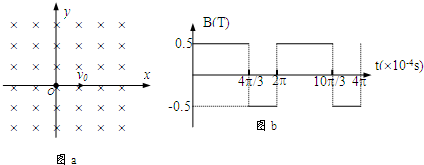
(1)t=×10-4s时刻,粒子的坐标.
(2)粒子从开始时刻起经多长时间到达y轴.
(3)粒子是否还可以返回原点?如果可以,则经多长时间返回原点?

分析:(1)由洛伦兹力提供向心力可以得到轨道半径,由轨道半径可得周期,由磁场的变化可以画出在第一段时间内粒子的运动轨迹,由运动轨迹的几何关系可得到粒子的坐标.
(2)依据第一问得到的结果,可以得到在第二,第三时间段内的运动轨迹,由图可知粒子恰好在第三段时间末到达y轴,由此可得时间
(3)依据磁场变化的周期性,可知粒子的运动也存在对应的周期性,可做粒子的轨迹图,由图可知其返回的时间.
(2)依据第一问得到的结果,可以得到在第二,第三时间段内的运动轨迹,由图可知粒子恰好在第三段时间末到达y轴,由此可得时间
(3)依据磁场变化的周期性,可知粒子的运动也存在对应的周期性,可做粒子的轨迹图,由图可知其返回的时间.
解答:解:(1)粒子进入磁场后在磁场中作圆周运动,设半径为R,周期为T,由洛仑兹力提供向心力,有
qvB=m
解得:R=
=
=0.4m
又:T=
=
=
=4π×10-4s
在磁场变化的第一段时间内,粒子运动的周期数为:N =
=
(个运动周期)
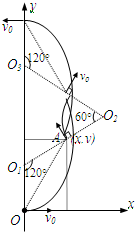
运动轨迹对应的圆心角为120°,作出粒子在磁场中运动的轨迹如图所示.
第一段时间末,粒子的坐标为:
x=Rcos30°=0.2
m,y=R+
sin30°=0.6m
所求时刻,粒子的坐标(0.2
m,0.6m)
(2)根据第(1)问可知,粒子在第一个磁场变化的时间段内时,运动了N1=
个周期,在第二个时间段内运动的周期数为N2=
=
(个周期)
所对应的运动轨迹圆心角为60°.运动轨迹如图所示.
第三个时间段内同样运动了:N3=
=
(个周期)
对应的圆心角为120°.
粒子运动的轨迹如图所示,粒子恰好在第三段时间末通过y轴.
故运动时间为t=
×10-3s
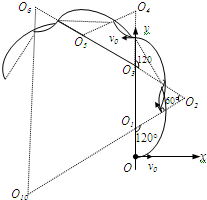
(3)粒子在磁场中作周期性运动,根据对称性和周期性,画出粒子的部分运动轨迹如图,其中O2、O6、O10构成一个正三边形.
故粒子在磁场中一共运动了6个大圆弧和3个小圆弧,故从原点出发到回到原点的总时间为
t'=6×
×10-4s+3×
×10-4s=π×10-3s
答:
(1)t=×10-4s时刻,粒子的坐标(0.2
m,0.6m).
(2)粒子从开始时刻起经运动时间为t=
×10-3s 到达y轴.
(3)粒子可以返回原点,所经历的时间为π×10-3s
qvB=m
| v2 |
| R |
解得:R=
| mv |
| qB |
| 2×103×10-4 |
| 0.5 |
又:T=
| 2πR |
| v |
| 2πm |
| qB |
| 2π×10-4 |
| 0.5 |

在磁场变化的第一段时间内,粒子运动的周期数为:N =
| ||
| 4π×104 |
| 1 |
| 3 |
运动轨迹对应的圆心角为120°,作出粒子在磁场中运动的轨迹如图所示.
第一段时间末,粒子的坐标为:
x=Rcos30°=0.2
| 3 |
. |
| O1A |
所求时刻,粒子的坐标(0.2
| 3 |
(2)根据第(1)问可知,粒子在第一个磁场变化的时间段内时,运动了N1=
| 1 |
| 3 |
| ||
| 4π×104 |
| 1 |
| 6 |
所对应的运动轨迹圆心角为60°.运动轨迹如图所示.
第三个时间段内同样运动了:N3=
| ||
| 4π×104 |
| 1 |
| 3 |
对应的圆心角为120°.
粒子运动的轨迹如图所示,粒子恰好在第三段时间末通过y轴.
故运动时间为t=
| π |
| 3 |
(3)粒子在磁场中作周期性运动,根据对称性和周期性,画出粒子的部分运动轨迹如图,其中O2、O6、O10构成一个正三边形.
故粒子在磁场中一共运动了6个大圆弧和3个小圆弧,故从原点出发到回到原点的总时间为
t'=6×
| 4π |
| 3 |
| 2π |
| 3 |

答:
(1)t=×10-4s时刻,粒子的坐标(0.2
| 3 |
(2)粒子从开始时刻起经运动时间为t=
| π |
| 3 |
(3)粒子可以返回原点,所经历的时间为π×10-3s
点评:本题重点是对磁场周期性的应用,磁场的周期性一定就会由粒子运动周期性的变化,故只要得到一个周期的运动轨迹,就可以重复画轨迹,直到得到想要的结果.本题由于粒子的运动轨迹比较复杂,故考察的难度相对较大.

练习册系列答案
相关题目
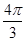 ´10-4s时刻,粒子的坐标。
´10-4s时刻,粒子的坐标。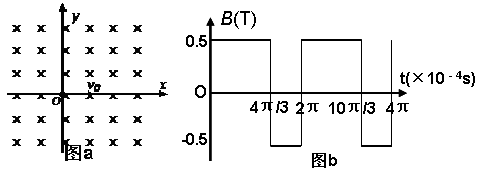
 ´10-4s时刻,粒子的坐标。
´10-4s时刻,粒子的坐标。