题目内容
如图所示,在游乐节目中,选手需要借助悬挂在高处的绳飞越对面的高台上. 一质量m=60kg的选手脚穿轮滑鞋以v0=7m/s的水平速度抓住竖直的绳开始摆动,选手可看作质点,这时,绳子的悬挂点到选手的距离L=6m.当绳摆到与竖直方向夹角θ=37°时,选手放开绳子。不考虑空气阻力和绳的质量.取重力加速度g="10m/s2," sin370=0.6,cos370=0.8.求: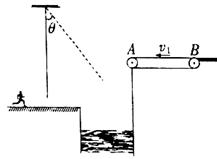
(1)选手放开绳子时的速度大小;
(2)选手放开绳子后继续运动到最高点时,刚好可以站到水平传送带A点, 传送带始终以v1=3m/s的速度匀速向左运动,传送带的另一端B点就是终点,且SAB=3.75m.若选手在传送带上不提供动力自由滑行,受到的摩擦阻力为自重的0.2倍,通过计算说明该选手是否能顺利冲过终点B,并求出选手在传送带上滑行过程中因摩擦而产生的热量Q。
(1)5m/s (2)x=4m>3.75m,所以可以顺利冲过终点;Q = 990J
解析试题分析:(1)据题意,当选手以v0=7m/s的水平速度抓住竖直的绳开始摆动,摆角为θ=37°时,据机械能守恒定律有:
经计算的v=5m/s
(2)当选手放手后在水平方向的速度为
vx=vcos37°=4m/s
则选手到达传送带上后,以4m/s的速度向右运动,则据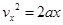
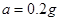
则选手滑动距离为x=4m>SAB=3.75m,所以选手可以通过传送带。
当选手在传送带上滑动过程中末速度为v1,由于选手做匀减速直线运动,则有: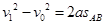
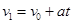
则选手在传送带上的运动时间为:t=1.5s
选手和传送带的相对位移为: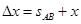
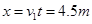
则选手在传送带上产生的热量为:
Q=fΔx=990J
考点:本题考查机械能守恒定律、运动的分解、运动学关系和热量的计算。

练习册系列答案
相关题目
 。(取g=10 m/s2)求:
。(取g=10 m/s2)求:
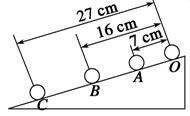
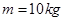 的货物(可视为质点)被机械杆向左推出,机械杆对货物的推力F为恒力,大小为
的货物(可视为质点)被机械杆向左推出,机械杆对货物的推力F为恒力,大小为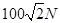 ,与水平面间夹角
,与水平面间夹角 ,行至B点时撤掉F,因水平面与皮带间有转角,货物经B点时速度会突减一半,传送带若不转动,货物到达顶端的C点时速度恰好为零,C点处的工人立刻将货物搬走。已知AB的长度L=16m,货物与水平面间的动摩擦因数
,行至B点时撤掉F,因水平面与皮带间有转角,货物经B点时速度会突减一半,传送带若不转动,货物到达顶端的C点时速度恰好为零,C点处的工人立刻将货物搬走。已知AB的长度L=16m,货物与水平面间的动摩擦因数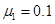 ,传送带BC的长度
,传送带BC的长度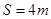 ,动传送带与水平面间倾角
,动传送带与水平面间倾角 ,(
,(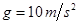 )试求:
)试求:
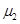 ;
; 的速度逆时针转动,传送带开始动转时恰好有一货箱到达了C点,工人却未能及时将其搬走而造成与下一个货箱在传送带上相撞。求这两个货物箱在传送带上相撞的位置到C点的距离
的速度逆时针转动,传送带开始动转时恰好有一货箱到达了C点,工人却未能及时将其搬走而造成与下一个货箱在传送带上相撞。求这两个货物箱在传送带上相撞的位置到C点的距离 。
。
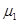 、木板与地面间的动摩擦因数
、木板与地面间的动摩擦因数 ;
;