Question

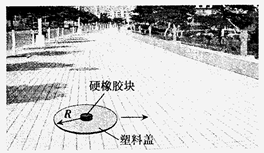
如图所示，由于街道上的圆形污水井盖破损，临时更换了一个稍大于井口的红色圆形平板塑料盖．为了测试因塑料盖意外移动致使盖上的物块滑落入污水井中的可能性，有人先后分别做了下面的实验．
甲实验：将一个可视为质点、质量为m的硬橡胶块置于塑料盖的圆心处，给塑料盖一个沿径向的瞬间水平冲量，使之获得一个水平向右的初速度．实验结果是硬橡胶块恰好与塑料盖分离．
乙实验：完成甲实验后，将塑料盖放回原处，仍将该硬橡胶块置于塑料盖的圆心处，然后用一水平向右的恒定拉力拉动塑料盖．
设硬橡胶块与塑料盖间的动摩擦因数为μ，塑料盖的质量为M、半径为R，假设塑料盖与地面之间的摩擦可忽略，井口的半径也约为R，且不计塑料盖的厚度．
（1）甲实验中，根据实验结果求：
①塑料盖的初速度大小为多少？
②硬橡胶块经过多少时间脱离塑料盖？
③通过计算说明硬橡胶块是落入井内还是落在地面上？
（2）在乙实验中，拉力F在什么范围内，才可以使硬橡胶块落入井内？

Answer 1

分析：（1）硬橡胶块与塑料盖恰好分离时，两者的共同速度为v，由系统动量守恒定律和系统能量关系求解．
对硬橡胶块用动量定理求解经过多少时间脱离塑料盖，取硬橡胶块分析，应用动能定理求解硬橡胶块是落入井内还是落在地面上．
（2）取硬橡胶块分析，应用牛顿第二定律和运动学公式求解分析．

解答：解：（1）①设塑料盖的初速度为v₀，硬橡胶块与塑料盖恰好分离时，两者的共同速度为v，由系统动量守恒定律得：Mv₀=（m+M）v
       由系统能量关系可得：μmgR=

1

2

Mv

2 0

-

1

2

（M+m）v²
       解得  v₀=

2(m+M)μgR M

       ②对硬橡胶块用动量定理：μmgt=mv 
    t=

2MR (M+m)μg

     
       ③设硬橡胶块与塑料盖恰好分离时，硬橡胶块移动的位移为x，
       取硬橡胶块分析，应用动能定理得：μmgx=

1

2

mv²
       可得：x=

MR

M+m

      所以x＜R，故硬橡胶块将落人污水井内
（2）能落入井内说明二者必然有相对滑动，其间的摩擦力为滑动摩擦力，所以：
       塑料盖的加速度a₁=

F-μmg

M

，
橡胶块的加速度a₂=

μmg

m

=μg
       设橡胶块经t₁时间脱离塑料盖，则由位移关系得：

1 2 a1t

2 1

-

1 2 a2t

2 1

=R
       又要求橡胶块落入井内，必有

1 2 a2t

2 1

＜R
       解得：F＞μmg+2μMg
答：（1）①塑料盖的初速度大小为

2(m+M)μgR M

②硬橡胶块经过

2MR (M+m)μg

时间脱离塑料盖
③硬橡胶块将落人污水井内
（2）在乙实验中，F＞μmg+2μMg，才可以使硬橡胶块落入井内．

点评：正确应用牛顿运动定律和功能关系列方程是解决这类问题的关键，尤其是弄清相互作用过程中的功能关系．