题目内容
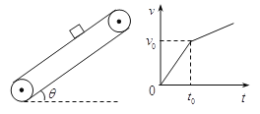
【题目】足够长的U型光滑导轨固定在倾角为30°的斜面上,导轨的宽度L=0.5m,其下端与R=1Ω的电阻连接,质量为m=0.2kg的导体棒(长度也为L)与导轨接触良好,导体棒及导轨电阻均不计,磁感应强度B=2T的匀强磁场垂直于导轨所在的平面,用一根与斜面平行的不可伸长的轻绳跨过定滑轮将导体棒和质量为M=0.5kg的重物相连,重物离地面足够高,使导体棒从静止开始沿导轨上滑,当导体棒沿导轨上滑t=2s时,其速度达到最大,取g=10m/s2,则导体棒从静止开始沿轨道上滑时间t=2s的过程中,电阻R上产生的焦耳热是多少?

【答案】15.2J
【解析】
速度最大时导体棒切割磁感线产生感应电动势:
E=BLvm……①
感应电流:
I=![]() …………………………………………………………………②
…………………………………………………………………②
安培力:
FA=BIL…………………………………………………………………③
导体棒达到最大速度时由平衡条件得:
Mg=mgsin30°+FA……………………④
联立解得
vm=4m/s………………………………………………………………⑤
以导体棒和重物为系统由动量定理得:
![]()
即
![]() …………………………………⑥
…………………………………⑥
解得2s内流过导体棒的电荷量
q=5.2C………………………………………⑦
电量
![]() ……………………………………………………………⑧
……………………………………………………………⑧
解得2s内导体棒上滑位移
x=5.2m…………………………………………⑨
由能量守恒定律得
![]() …………………⑩
…………………⑩
解得
Q=15.2J…………………………………………………………………

练习册系列答案
 开心试卷期末冲刺100分系列答案
开心试卷期末冲刺100分系列答案 双基同步导航训练系列答案
双基同步导航训练系列答案 黄冈小状元同步计算天天练系列答案
黄冈小状元同步计算天天练系列答案
相关题目