题目内容
12.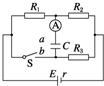 如图所示,电源电动势E=6V,内阻r=1Ω,电阻R1=2Ω,R2=3Ω,R3=7.5Ω,电容器的电容C=5 μF.开关S原来断开,现在合上开关S到电路稳定,试问这一过程中通过电流表的电荷量是多少?
如图所示,电源电动势E=6V,内阻r=1Ω,电阻R1=2Ω,R2=3Ω,R3=7.5Ω,电容器的电容C=5 μF.开关S原来断开,现在合上开关S到电路稳定,试问这一过程中通过电流表的电荷量是多少?
分析 开关S断开时,电容器的电压等于R2的电压,根据闭合电路欧姆定律求出电压,再根据Q=CU求出其带电量.S闭合时,电路稳定时电容器所在电路没有电流,电容器的电压就是R1的电压,根据闭合电路欧姆定律求出电路中的总电流,由欧姆定律求出电容器的电压,由Q=CU求解其电量.分析电容器极板电荷的变化,从而得到流过电流表A的电荷量.
解答 解:S断开时的等效电路如图甲所示,电容器C两端电压U为电阻R2两端电压U2,则
U2=$\frac{E}{{R}_{1}+{R}_{2}+r}$•R2=3V.
电容器C的电荷量 Q=CU=CU2=1.5×10-5 C.且a板带正电,b板带负电.
S闭合时的等效电路如图乙所示,电容器C两端电压U′为电阻R1两端电压U′1.
有R外$\frac{{R}_{3}({R}_{1}+{R}_{2})}{{R}_{3}+{R}_{1}+{R}_{2}}$=3Ω,
电阻R1中的电流 I′1=$\frac{E}{{R}_{外}+r}$•$\frac{{R}_{外}}{{R}_{1}+{R}_{2}}$=0.9 A
电阻R1两端电压 U′1=I′1R1=1.8 V,
电容器C的电荷量 Q′=CU′=CU′1=9.0×10-6 C.
且a板带负电,b板带正电.
通过电流表的电荷量为△Q=Q+Q′=2.4×10-5 C.
答:通过电流表的电荷量为2.4×10-5 C.
点评 本题主要考查了闭合电路欧姆定律的直接应用,关键要同学们能理清电路的结构,明确电容器的电压与哪部分电路的电压相等,要知道电路稳定时,电容器所在电路没有电流,其电压与所并联的电路两端的电压相等.

练习册系列答案
 黎明文化寒假作业系列答案
黎明文化寒假作业系列答案
相关题目
2. 如图所示,分别在M、N两点固定放置两个点电荷+Q和-2Q,以M、N连线的中点O为圆心的圆周上有A、B、C、D四点.下列说法正确的是( )
如图所示,分别在M、N两点固定放置两个点电荷+Q和-2Q,以M、N连线的中点O为圆心的圆周上有A、B、C、D四点.下列说法正确的是( )
 如图所示,分别在M、N两点固定放置两个点电荷+Q和-2Q,以M、N连线的中点O为圆心的圆周上有A、B、C、D四点.下列说法正确的是( )
如图所示,分别在M、N两点固定放置两个点电荷+Q和-2Q,以M、N连线的中点O为圆心的圆周上有A、B、C、D四点.下列说法正确的是( )| A. | A点电场强度小于B点电场强 | |
| B. | C点电场强度与D点电场强度相同 | |
| C. | A点电势高于B点电势 | |
| D. | 将某正电荷从C点移到O点,电场力做正功 |
3. 如图所示,桌面离地高度为h,质量为m的小球,从离桌面H高处由静止下落.此过程中小球的重力势能( )
如图所示,桌面离地高度为h,质量为m的小球,从离桌面H高处由静止下落.此过程中小球的重力势能( )
 如图所示,桌面离地高度为h,质量为m的小球,从离桌面H高处由静止下落.此过程中小球的重力势能( )
如图所示,桌面离地高度为h,质量为m的小球,从离桌面H高处由静止下落.此过程中小球的重力势能( )| A. | 增加mgh | B. | 增加mg(H+h) | C. | 减少 mgH | D. | 减少mg(H+h) |
20.如图是某质点运动的v-t图象,由图象倒得的正确结果是( )


| A. | 0~2s内的位移大小是3m | |
| B. | 0~4s内的平均速度是2m/s | |
| C. | 0~1s内的加速度大小大于2~4s内的加速度大小 | |
| D. | 0~1s内的运动方向与2~4s内的运动方向相反 |
4.已知月球半径为R,飞船在距月球表面高度为R的圆轨道上飞行,周期为T,万有引力常量为G,下列说法正确的是( )
| A. | 月球表面重力加速度为g=$\frac{32{π}^{2}R}{{T}^{2}}$ | |
| B. | 月球第一宇宙速度为$\frac{4πR}{T}$ | |
| C. | 月球密度为$\frac{3π}{G{T}^{2}}$ | |
| D. | 月球质量为$\frac{24π}{G{T}^{2}}$ |
2.如下图甲所示,质量为2.955kg的木块随水平传送带(足够长)一起向右匀动,一颗质量为0.045kg的子弹水平向左射人木块中(未射出),子弹运动的v-t图象如下图乙所示,已知木块与传送之间的动摩擦因数μ=0.1,g取10m/s2,以向左为运动正方向,则以下分析正确的是( )
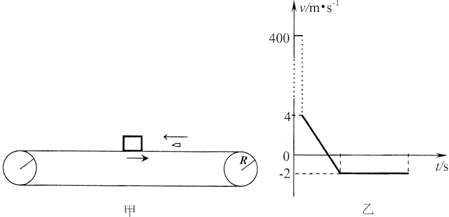

| A. | 子弹刚击中木块后二者的共同速度为2m/s | |
| B. | 子弹击中木块后再过6s木块重新与传送带达到共同速度2m/s | |
| C. | 子弹击中木块后向左运动的最大位移为8m | |
| D. | 木块与传送带摩擦生热36 J |
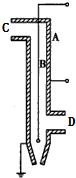 利用静电除尘器可以消除空气中的粉尘,静电除尘器由金属管A和悬在管中的金属丝B组成,B附近的气体分子被电离成为电子和正离子,粉尘吸附电子后被吸附到A上,最后在重力作用下落入下面的漏斗中.A和B分别接到高压电源的正极和负极,其装置示意图如图所示,含粉尘的高温气体从管口D(填“C”或“D”)进入金属管A内,A、B之间有很强的电场,距B越近,场强越大.
利用静电除尘器可以消除空气中的粉尘,静电除尘器由金属管A和悬在管中的金属丝B组成,B附近的气体分子被电离成为电子和正离子,粉尘吸附电子后被吸附到A上,最后在重力作用下落入下面的漏斗中.A和B分别接到高压电源的正极和负极,其装置示意图如图所示,含粉尘的高温气体从管口D(填“C”或“D”)进入金属管A内,A、B之间有很强的电场,距B越近,场强越大.