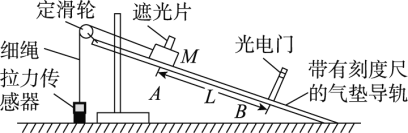
题目内容
【题目】长为L的轻杆可绕O在竖直平面内无摩擦转动，质量为M的小球A固定于杆端点，质点为m的小球B固定于杆中点，且M=2m，开始杆处于水平，由静止释放，当杆转到竖直位置时
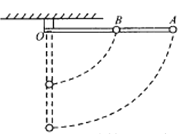
A. 轻杆对球A做正功
B. 球A在最低点速度为
C. OB杆的拉力小于BA杆的拉力
D. 轻杆对球B做功
【答案】AD
【解析】
A、B小球随杆转动，设杆转到竖直位置时线速度分别为
,
，因为球A、B的角速度相同，所以线速度
，应用机械能守恒，
，
解得
;
故B错
在转动过程中设杆对B求做功为WB，则根据动能定理可求得：
解得：
故D对
由于系统机械能守恒，轻杆对B做负功，则轻杆对A做正功，故A对；
研究球B，在转动过程中，球B受到重力、OB杆的拉力和BA杆的拉力，这三个力的合力提供指向O点的向心力，所以OB杆的拉力要大于BA杆的拉力，故C错
故选AD
练习册系列答案
相关题目
