题目内容
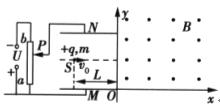
【题目】如图所示，在xoy平面直角坐标系第一象限内分布有垂直向外的匀强磁场，磁感应强度大小B=2.5×10﹣2T，在第二象限紧贴y轴和x轴放置一对平行金属板MN（中心轴线过y轴），极板间距d=0.4m，极板与左侧电路相连接．通过移动滑动头P可以改变极板MN间的电压．a、b为滑动变阻器的最下端和最上端（滑动变阻器的阻值分布均匀），a、b两端所加电压U= 
．在MN中心轴线上距y轴距离为L=0.4m处有一粒子源S，沿x轴正方向连续射出比荷为
=4.0×106C/kg，速度为vo=2.0×104m/s带正电的粒子，粒子经过y轴进入磁场后从x轴射出磁场（忽略粒子的重力和粒子之间的相互作用）．
（1）当滑动头P在ab正中间时，求粒子射入磁场时速度的大小．
（2）当滑动头P在ab间某位置时，粒子射出极板的速度偏转角为α，试写出粒子在磁场中运动的时间与α的函数关系，并由此计算粒子在磁场中运动的最长时间．
【答案】（1）2.1×104m/s．（2）
，最长时间为2.6×10﹣5s
【解析】解：（1）当滑动头P在ab正中间时，极板间电压U′= 
，粒子在电场中做类平抛运动，设粒子射入磁场时沿y轴方向的分速度为vy：
①
vy=at②
L=v0t③
粒子射入磁场时速度的大小设为
④
联立解得： 
⑤
（2）当滑动头P在a端时，粒子在磁场中运动的速度大小为v0，有
⑥
解得：R0=
=0.2m
设粒子射出极板时速度的大小为v，偏向角为α，在磁场中圆周运动半径为R．根据速度平行四边形可得：
⑦
又
，得R=
⑧
由⑥⑦⑧可得： 
⑨
粒子在磁场中做圆周运动的轨迹如图所示
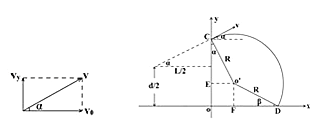
圆心为O′，与x轴交点为D，
设∠O′DO=β，根据几何关系：
⑩
又： 
解得：sinα=sinβ，得β=α
粒子在磁场中运动的周期为T： 
粒子在磁场中轨迹对应的圆心角为
则粒子在磁场中运动的时间：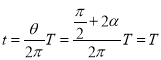 
，得t=
由此结果可知，粒子射入磁场时速度偏转角α越大，则粒子在磁场中运动的时间就越大．假设极板间电压为最大值
时粒子能射出电场，则此粒子在磁场中运动的时间最长．
由（1）问规律可知当滑动头P在b端时，粒子射入磁场时沿y方向的分速度： 
y方向偏距：ym=
，说明粒子可以射出极板．此时粒子速度偏转角最大，设为αm，则
tanam=
，得
故粒子在磁场中运动的最长时间： 
，得
代入数值得：tm≈2.6×10﹣5s
