题目内容
【题目】2007年10月24日，中国首颗探月卫星“嫦娥一号”在西昌卫星发射中心发射升空，准确进入预定轨道．随后，“嫦娥一号”经过变轨和制动成功进入环月轨道．如图所示，阴影部分表示月球，设想飞船在距月球表面高度为3R的圆形轨道Ⅰ上作匀速圆周运动，到达A点时经过暂短的点火变速，进入椭圆轨道Ⅱ，在到达轨道Ⅱ近月点B点时再次点火变速，进入近月圆形轨道Ⅲ，而后飞船在轨道Ⅲ上绕月球作匀速圆周运动．已知月球半径为R，月球表面的重力加速度为g0．不考虑其它星体对飞船的影响，求：
（1）飞船在轨道Ⅰ、Ⅲ的速度之比．
（2）飞船从轨道Ⅱ上远月点A运动至近月点B所用的时间．
（3）如果在Ⅰ、Ⅲ轨道上有两只飞船，它们绕月球飞行方向相
同，某时刻两飞船相距最近（两飞船在月球球心的同侧，且两飞船与月球球心在同一直线上），则经过多长时间，他们又会相距最近？
【答案】(1) 
(2) 
(3) 
【解析】试题分析：根据万有引力提供圆周运动向心力，由半径与关系求得速度之比；根据开普勒行星定律由半长轴的关系求得周期，从远月点飞到近月点所用时间为椭圆轨道的一半周期；相距最近时，两飞船中运得快的比运动得慢的多绕月飞行n周，根据角速度关系求解所用时间即可。
（1）由万有引力提供向心力有：
，解得：
所以：
（2）设飞船在轨道I上的运动周期为T1，在轨道I有：
在月球表面有： 
由以上可得：
设飞船在轨道II上的运动周期T2，而轨道II的半长轴为2.5R，
根据开普勒定律得：
可解得：
所以飞船从A到B的飞行时间为：
（3）设飞船在轨道I上的角速度为ω1、在轨道III上的角速度为ω3，有：
所以
设飞飞船再经过t时间相距最近，有：ω3t﹣ω1t=2nπ
所以
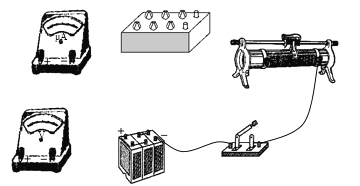
【题目】在“探究求合力的方法”实验中，现有木板、白纸、图钉、橡皮筋、细绳套和一只弹簧测力计．
(1)为了完成实验，某同学另找来一根弹簧，先测量其劲度系数，得到的实验数据如下表：
弹力F(N) | 0.50 | 1.00 | 1.50 | 2.00 | 2.50 | 3.00 | 3.50 |
伸长量 x(10－2 m) | 0.74 | 1.80 | 2.80 | 3.72 | 4.60 | 5.58 | 6.42 |
根据表中数据在作出F－x图象__________并求得该弹簧的劲度系数k＝________N/m；
(2)某次实验中，弹簧测力计的指针位置如图甲所示，其读数为________N；同时利用(1)中结果获得弹簧上的弹力值为2.50 N，请在图乙中画出这两个共点力的合力F合的图示______________；
(3)由图得到F合＝________N.
