题目内容
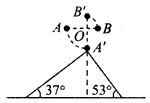
如图所示，轻直杆长为2 m，两端各连着一个质量为1 kg的小球A、B，直杆绕着O点以ω=8 rad/s逆时针匀速转动，直杆的转动与直角斜面体在同一平面内。OA=1.5 m，A轨迹的最低点恰好与一个直角斜面体的顶点重合，斜面的底角为37°和53°，取g=10 m/s2。求：
（1）当A球通过最低点时，求B球对直杆的作用力；
（2）若当A球通过最低点时，两球脱离直杆（不影响两球瞬时速度，此后两球不受杆影响），此后B球恰好击中斜面底部，且两球跟接触面碰后小反弹，试求B球在空中飞行的时间；
（3）在（2）的情形下，求两球落点间的距离。
（1）当A球通过最低点时，求B球对直杆的作用力；
（2）若当A球通过最低点时，两球脱离直杆（不影响两球瞬时速度，此后两球不受杆影响），此后B球恰好击中斜面底部，且两球跟接触面碰后小反弹，试求B球在空中飞行的时间；
（3）在（2）的情形下，求两球落点间的距离。
解：（1）设杆对B球的作用力F向F，有mg+F=mω2·OB
解得F=22N，即杆对B的作用力为22 N，方向向下
由牛顿第三定律，B球对杆的作用力F'=22 N，方向向上
（2）脱离直杆时vA=ωOA=12 m/s，vB=ωOB=4 m/s
设在空中飞行时间为t，则有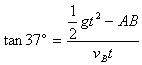
解得t=1s
（3）B的水平位移xB=vBt=4 m
A的竖直位移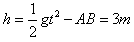
A的水平位移
，A直接落在地面上
因此两球落点间距为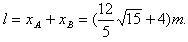
解得F=22N，即杆对B的作用力为22 N，方向向下
由牛顿第三定律，B球对杆的作用力F'=22 N，方向向上
（2）脱离直杆时vA=ωOA=12 m/s，vB=ωOB=4 m/s
设在空中飞行时间为t，则有
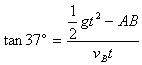
解得t=1s
（3）B的水平位移xB=vBt=4 m
A的竖直位移
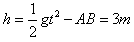
A的水平位移
，A直接落在地面上因此两球落点间距为
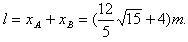
练习册系列答案
阅读快车系列答案
相关题目
如图所示，虚线上方有场强为E的匀强电场，方向竖直向下，虚线上下有磁感应强度相同的匀强磁场，大小为B，方向垂直纸面向外，ab是一根长为L的绝缘细杆，沿电场线放置在虚线上方的场中，b端在虚线上．将一套在杆上的带正电的轻小球，带电量为q，质量为m，从a端由静止释放，小球到达b端前已做匀速运动．已知小球与绝缘杆间的动摩擦因数为μ，小球重力忽略不计，当小球脱离杆进入虚线下方的磁场，求：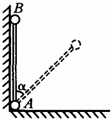
如图所示，轻质细杆竖直位于相互垂直的光滑墙壁和光滑地板交界处，质量均为m的两个小球A与B固定在长度为L的轻质细杆两端，小球半径远小于杆长，小球A位于墙角处．若突然发生微小的扰动使杆沿同一竖直面无初速倒下，不计空气阻力，杆与竖直方向成α角（α＜arccos 2/3）时，求：
（2012?黄埔区模拟）如图所示，小球a的质量为M，被一根长为L=0.5m的可绕O轴自由转动的轻质细杆固定在其端点，同时又通过绳跨过光滑定滑轮与另一个小球b相连，整个装置平衡时杆和绳与竖直方向的夹角均为30°．若将小球a拉水平位置（杆呈水平状态）开始释放，不计摩擦，重力加速度g取10m/s2，竖直绳足够长，求当杆转动到竖直位置时，小球b的速度大小．
长为2L的轻杆从中点处弯成互相垂直的两部分，搭在光滑水平轴O上，如图所示，A端固定质量为M小球，B端固定质量为m的小球，在OB中点也固定一质量为m小球．现在将OA由水平静止释放，当OA竖直时（OB水平）开始回转，不计一切阻力，则M、m关系是（ ）