题目内容
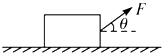水平地面上有一木箱，木箱与地面之间的动摩擦因数为μ（0＜μ＜1）．现对木箱施加一拉力F，使木箱做匀速运动．设F的方向与水平面夹角为θ，如图，在θ从0逐渐增大到90°的过程中，木箱的速度保持不变，则（ ）| A、F一直增大 | B、F先增大后减小 | C、F的功率不变 | D、F的功率减小 |
分析：在θ从0逐渐增大到90°的过程中，木箱的速度保持不变，说明物体受力始终平衡，受力分析后正交分解表示出拉力F，应用数学方法讨论F的变化．而功率P=Fv可以判断其变化．
解答：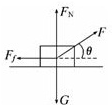
解：对物体受力分析如图：
因为物体匀速运动，水平竖直方向均受力平衡：
水平方向：Fcosθ=μ（mg-Fsinθ） ①
竖直方向：FN+Fsinθ=mg ②
解得：F=
令：sinβ=
，cosβ=
即：tanβ=
则：F=
=
θ从0逐渐增大到90°的过程中，在θ＜β前：cos（θ-β）逐渐变大，所以F逐渐减小．
在θ＞β后：cos（θ-β）逐渐变小，所以F逐渐增大，故AB错误；
P=Fvcosθ=
当θ增大时，tanθ增大，故P减小，故C错误，D正确．
故选：D．
解：对物体受力分析如图：因为物体匀速运动，水平竖直方向均受力平衡：
水平方向：Fcosθ=μ（mg-Fsinθ） ①
竖直方向：FN+Fsinθ=mg ②
解得：F=
| μmg |
| cosθ+μsinθ |
令：sinβ=
| 1 | ||
|
| μ | ||
|
| 1 |
| μ |
则：F=
| μmg | ||
(sinβcosθ+cosβsinθ)
|
| μmg | ||
cos(θ-β)
|
θ从0逐渐增大到90°的过程中，在θ＜β前：cos（θ-β）逐渐变大，所以F逐渐减小．
在θ＞β后：cos（θ-β）逐渐变小，所以F逐渐增大，故AB错误；
P=Fvcosθ=
| μmg |
| 1+μtanθ |
当θ增大时，tanθ增大，故P减小，故C错误，D正确．
故选：D．
点评：本题为平衡条件的应用问题，受力分析后应用平衡条件求解即可，难点在于研究对象的选择和应用数学方法讨论拉力F的变化，难度不小，需要细细品味．
练习册系列答案
期末1卷素质教育评估卷系列答案
相关题目
（2009?宁夏）水平地面上有一木箱，木箱与地面之间的动摩擦因数为μ（0＜μ＜1）．现对木箱施加一拉力F，使木箱做匀速直线运动．设F的方向与水平面夹角为θ，如图，在θ从0逐渐增大到90°的过程中，木箱的速度保持不变，则（ ）
如图所示，水平地面上有一木箱，受到水平拉力F的作用，F随时间t正比增大，即F=kt（k为常数）．则木箱所受摩擦力f随时间t的变化图象正确的是（ ）
（2010?洛阳模拟）水平地面上有一木箱，木箱与地面之间的动摩擦因数为μ，现对木箱施加一拉力F，使木箱做匀速直线运动．设F的方向与水平面夹角为θ，如图所示，在θ从0°逐渐增大到90°的过程中，木箱的速度保持不变，则（ ）