题目内容
10.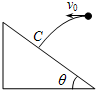 以初速度v0向一倾角为θ的斜面水平抛出一个小球,经过一段时间,小球垂直落在斜坡上的C点,不计空气的阻力,重力加速度为g,则( )
以初速度v0向一倾角为θ的斜面水平抛出一个小球,经过一段时间,小球垂直落在斜坡上的C点,不计空气的阻力,重力加速度为g,则( )| A. | 小球从抛出到落到斜面上的时间为$\frac{{v}_{0}cotθ}{g}$ | |
| B. | 小球从抛出到落到斜面上的时间为$\frac{{v}_{0}tanθ}{g}$ | |
| C. | 小球落到斜面上的速度大小为$\frac{{v}_{0}}{tanθ}$ | |
| D. | 小球落到斜面上的速度大小为$\frac{{v}_{0}}{cosθ}$ |
分析 小球垂直落在斜坡上的C点,速度方向与斜面垂直,根据平行四边形定则求出此时的速度大小和竖直分速度,结合速度时间公式求出小球抛出到落到斜面上的时间.
解答 解:A、根据平行四边形定则知:$tanθ=\frac{{v}_{0}}{{v}_{y}}$,则有:${v}_{y}=\frac{{v}_{0}}{tanθ}=gt$,解得:t=$\frac{{v}_{0}}{gtanθ}$,故A正确,B错误.
C、根据平行四边形定则知,小球落在斜面上的速度为:$v=\frac{{v}_{0}}{sinθ}$,故C、D错误.
故选:A.
点评 本题考查了有限制条件的平抛运动,抓住速度与斜面垂直,结合平行四边形定则进行求解,难度不大.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
18.唐诗中“看山恰似走来迎”一句中,作者选择的参照系是( )
| A. | 地面 | B. | 行船 | C. | 山 | D. | 天空 |
5. 一个矩形线圈abcd,已知ab为L1,ad为L2,在磁感应强度为B的匀强磁场中绕OO′轴以角速度ω(从图位置开始)匀速转动,则线圈中感应电动势的表达式为( )
一个矩形线圈abcd,已知ab为L1,ad为L2,在磁感应强度为B的匀强磁场中绕OO′轴以角速度ω(从图位置开始)匀速转动,则线圈中感应电动势的表达式为( )
 一个矩形线圈abcd,已知ab为L1,ad为L2,在磁感应强度为B的匀强磁场中绕OO′轴以角速度ω(从图位置开始)匀速转动,则线圈中感应电动势的表达式为( )
一个矩形线圈abcd,已知ab为L1,ad为L2,在磁感应强度为B的匀强磁场中绕OO′轴以角速度ω(从图位置开始)匀速转动,则线圈中感应电动势的表达式为( )| A. | $\frac{1}{2}$BL1L2ωsinωt | B. | $\frac{1}{2}$BL1L2ωcosωt | C. | BL1L2ωsinωt | D. | BL1L2ωcosωt |
15.一个力分解为两个分力,下列情况中,说法中正确的是( )
| A. | 一个2 N的力可分解为7 N和4 N的两个分力 | |
| B. | 一个2 N的力可分解为9 N和9 N的两个分力 | |
| C. | 一个6 N的力可分解为4 N和12 N的两个分力 | |
| D. | 一个8 N的力可分解为4 N和3 N的两个分力 |
2.在已接电源的闭合电路里,关于电源的电动势、内电压、外电压的关系应是( )
| A. | 如外电压增大,则内电压增大,电源电动势也会随之增大 | |
| B. | 电路中并联的用电器增加时,路端电压一定增大 | |
| C. | 把伏特表直接和电源连接时,伏特表的示数总小于电源电动势 | |
| D. | 如外电压增大,则内电压减小,电源的电动势始终为二者之和,保持恒量 |
19.对物体运动的描述,以下说法正确的是( )
| A. | 直线运动的加速度可能变化 | |
| B. | 加速度方向不变的运动一定是匀变速直线运动 | |
| C. | 加速度减小的运动是减速运动,加速度增加的运动是加速运动 | |
| D. | 向左匀速直线运动的物体,当获得向右的合力时,将立即向右运动 |
20.物体做变速直线运动,某时刻的速度为3m/s,1s后速度的大小变为7m/s,在这1s内该物体的( )
| A. | 平均加速度大小只有一个值 | |
| B. | 平均加速度大小有多个值,各个值难以确定 | |
| C. | 速度的变化量可能小于初速度 | |
| D. | 速度的变化量可能大于末速度 |
