题目内容
在如图所示的装置中，PQM和P'Q'M'是两根固定的平行、光滑金属轨道，其中PQ和P'Q'水平而QM和Q'M'竖直，它们之间的距离均为L．质量为m、电阻为R的光滑金属棒ab垂直于PQ放置在水平轨道上，在它的中点系着一根柔软轻绳，轻绳通过一个被固定的轻小的定滑轮在另一端系住一个质量为m的物块A，定滑轮跟水平轨道在同一个平面内，轻绳处于绷直状态．另一根质量为m、电阻为R的金属棒cd垂直于QM和Q'M'紧靠在竖直轨道上，它在运动过程中始终跟轨道接触良好．整个装置处在水平向右的、磁感应强度为B的匀强磁场中．已知重力加速度为g，轨道和轻绳足够长，不计其余各处摩擦和电阻．现同时由静止释放物块A和金属棒cd，当物块A的速度达到某个值时，cd棒恰好能做匀速运动．求：
（1）cd棒匀速运动的速度大小；
（2）运动过程中轻绳产生的张力的大小；
（3）若cd棒从静止释放到刚达到最大速度的过程中产生的焦耳热为W，求此过程中cd棒下落的距离．
【答案】分析：（1）对cd棒受力分析，受安培力和重力作用，当匀速运动时，重力和安培力相等，由此可正确解答；
（2）设绳子上的拉力为T，对物块和金属棒分别利用牛顿第二定律列方程可正确解答；
（3）以cd棒为研究对象，利用动能定律列方程可正确解答．
解答：解：（1）cd棒匀速运动时，所受安培力跟重力相平衡，令此时回路中的电流为I，cd棒的速度为v，有：
BIL=mg
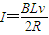
由以上两式可解得：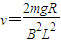
．
答：cd棒匀速运动的速度大小：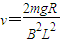
．
（2）令细绳产生的张力大小为T，物块的加速度大小为a，由牛顿第二定律：
对物块有：T-mg=ma
对ab棒有：T=ma
由以上两式可解得：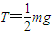
．
运动过程中轻绳产生的张力的大小为：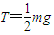
．
（3）由能量的转化和守恒定律有：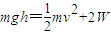
可解得：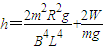
．
答：此过程中cd棒下落的距离为：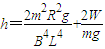
．
点评：本题考查了电磁感应与力学和功能关系的结合，是考查学生基础知识的好题．
（2）设绳子上的拉力为T，对物块和金属棒分别利用牛顿第二定律列方程可正确解答；
（3）以cd棒为研究对象，利用动能定律列方程可正确解答．
解答：解：（1）cd棒匀速运动时，所受安培力跟重力相平衡，令此时回路中的电流为I，cd棒的速度为v，有：
BIL=mg
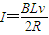
由以上两式可解得：
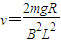．答：cd棒匀速运动的速度大小：
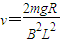．（2）令细绳产生的张力大小为T，物块的加速度大小为a，由牛顿第二定律：
对物块有：T-mg=ma
对ab棒有：T=ma
由以上两式可解得：
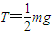．运动过程中轻绳产生的张力的大小为：
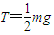．（3）由能量的转化和守恒定律有：
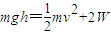
可解得：
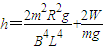．答：此过程中cd棒下落的距离为：
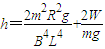．点评：本题考查了电磁感应与力学和功能关系的结合，是考查学生基础知识的好题．
练习册系列答案
相关题目
在如图所示的装置中，A、B、C、D为四个平行正对的金属板，其中B板和C板上开有小孔，分别与两个电源相连，B和A两板间的电压为U，C和D两板间电压为2U，从靠近A板的F处释放出一个无初速度的电子，电荷量为e．关于电子的运动，下列描述中哪些是正确的（ ）
（2011?广元模拟）在如图所示的装置中，电源电动势为E，内阻不计，定值电阻为R1，滑动变阻器总值为R2，置于真空中的平行板电容器水平放置，极板间距为d．处在电容器中的油滴A恰好静止不动，此时滑动变阻器的滑片P位于中点位置．
在如图所示的装置中，木块B与水平桌面的接触是光滑的，子弹A沿水平方向射入木块后留在木块内．从子弹射向木块到木块将弹簧压缩到最短的全过程中，下列说法正确
（2007?苏州二模）处在激发态的氢原子向能量较低的状态跃迁时会发出一系列不同频率的光，称为氢光谱．氢光谱线的波长可以用下面的巴耳末-里德伯公式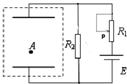
在如图所示的装置中，电源电动势为E，内阻不计，R2为定值电阻，滑动变阻器的滑片P位于中点位置时油滴A恰好静止不动，如将滑片P向下滑，油滴将（ ）