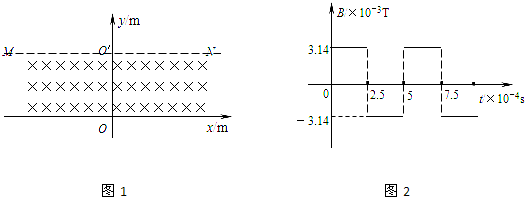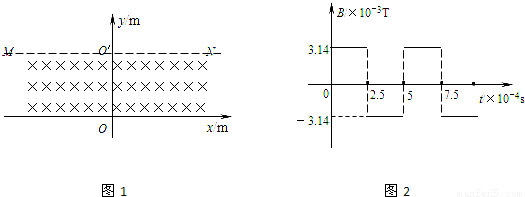题目内容
如图1所示，在y=0和y=0.9m之间有垂直纸面方向的匀强磁场，MN为磁场区域的上边界，磁场在x轴方向范围足够大．磁感应强度的变化如图2，取垂直纸面向里为正方向．现有一带负电的粒子，质量为m=4.8×10-18kg，带电量为q=3.2×10-12C，在t=0时刻以速度v0=6.28×102m/s从O点沿y轴正方向进入磁场区域，粒子重力不计．求：
（1）粒子在磁场中做圆周运动的周期和半径；
（2）画出0～5×10-4s内粒子的运动轨迹；
（3）粒子在t=5×10-4s时的位置坐标；
（4）粒子通过磁场区域的时间．
（1）粒子在磁场中做圆周运动的周期和半径；
（2）画出0～5×10-4s内粒子的运动轨迹；
（3）粒子在t=5×10-4s时的位置坐标；
（4）粒子通过磁场区域的时间．
分析：（1）粒子在磁场中做圆周运动，洛伦兹力提供向心力，写出公式即可求得圆周运动的半径和周期；
（2）一个磁场变化周期的
正好是粒子在磁场中做圆周运动周期的
；
（3）根据转过的角度关系计算即可；
（4）因y=0.9m，所以粒子通过磁场区域的时间为3个磁场变化周期，代人数据即可．
（2）一个磁场变化周期的
| T/ |
| 2 |
| T |
| 12 |
（3）根据转过的角度关系计算即可；
（4）因y=0.9m，所以粒子通过磁场区域的时间为3个磁场变化周期，代人数据即可．
解答：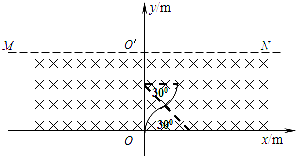
解：
（1）由洛伦兹力提供向心力 qvB=
可得r=
=
m=0.3m
T=
=
s=3×10-3s
（2）一个磁场变化周期的
正好是粒子在磁场中做圆周运动周期的
，0～5×10-4s内的轨迹如图：
（3）如图可知每经一个磁场变化周期的
正好是粒子在磁场中做圆周运动周期的
一个周期T′内粒子在x、y方向前进距离分别为：x=0.6（1-
/2）m，y=0.3m
粒子在t=5×10-4s时的位置坐标[0.6（1-
/2）m，0.3m]
（4）因y=0.9m，所以粒子通过磁场区域的时间为3个磁场变化周期，
粒子通过磁场区域的时间t=3T′=1.5×10-3s
答：（1）粒子在磁场中做圆周运动的周期是3×10-3s，半径是0.3m；
（2）画出0～5×10-4s内粒子的运动轨迹如图；
（3）粒子在t=5×10-4s时的位置坐标[0.6（1-
/2）m，0.3m]；
（4）粒子通过磁场区域的时间1.5×10-3s．
解：（1）由洛伦兹力提供向心力 qvB=
| mv2 |
| r |
可得r=
| mv |
| qB |
| 4.8×10-18×6.28×102 |
| 3.2×10-12×3.14×10-3 |
T=
| 2πm |
| qB |
| 2π×4.8×10-18 |
| 3.2×10-12×3.14×10-3 |
（2）一个磁场变化周期的
| T/ |
| 2 |
| T |
| 12 |
（3）如图可知每经一个磁场变化周期的
| T/ |
| 2 |
| T |
| 12 |
一个周期T′内粒子在x、y方向前进距离分别为：x=0.6（1-
| 3 |
粒子在t=5×10-4s时的位置坐标[0.6（1-
| 3 |
（4）因y=0.9m，所以粒子通过磁场区域的时间为3个磁场变化周期，
粒子通过磁场区域的时间t=3T′=1.5×10-3s
答：（1）粒子在磁场中做圆周运动的周期是3×10-3s，半径是0.3m；
（2）画出0～5×10-4s内粒子的运动轨迹如图；
（3）粒子在t=5×10-4s时的位置坐标[0.6（1-
| 3 |
（4）粒子通过磁场区域的时间1.5×10-3s．
点评：该题考查带电粒子在匀强磁场中的偏转，一个磁场变化周期的
正好是粒子在磁场中做圆周运动周期的
是该题的特殊的地方，注意到即可．
| T/ |
| 2 |
| T |
| 12 |
练习册系列答案
阅读快车系列答案
相关题目
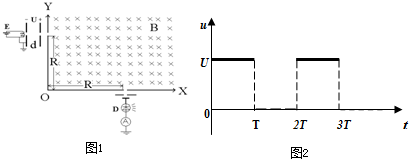
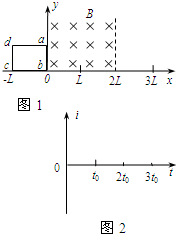如图1所示，在0≤x≤2L的区域内存在着匀强磁场，磁场方向垂直于xOy平面（纸面）向里，具有一定电阻的矩形线框abcd位于xOy平面内，线框的ab边与y轴重合，bc边长为L．设线框从t=0时刻起在外力作用下由静止开始沿x轴正方向做匀速运动，在图2坐标系中画出线框中的感应电流i（取顺时针方向的电流为正）随时间t变化的函数图象．
