题目内容
 如图所示,重100N的物体,用轻质细绳a和b悬挂,绳a水平、绳b与水平方向成60°角,试回答下列问题:
如图所示,重100N的物体,用轻质细绳a和b悬挂,绳a水平、绳b与水平方向成60°角,试回答下列问题:
(1)以结点O为研究对象,试画出其受力示意图.
(2)求绳a、b对重物的拉力Ta、Tb大小.
 解:
解:(1)结点O受到三个拉力作用:重物的拉力、绳a和b的拉力.作出受力示意图如图.
(2)由平衡条件,有:
Tbcos60°-Ta=0 …①
Tbsin60°-G=0 …②
∴由①②式,解得:
Tb=
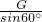 =
=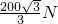
Ta=Gcot60°=
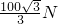
答:
(1)以结点O为研究对象,受力示意图如图.
(2)绳a、b对重物的拉力Ta、Tb大小分别为
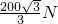 和
和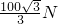 .
.分析:(1)结点O受到三个拉力作用:重物的拉力、绳a和b的拉力.作出受力示意图.
(2)根据平衡条件运用正交分解法求出绳a、b对重物的拉力Ta、Tb大小.
点评:本题是简单的力平衡问题,常常以结点O为研究对象,分析受力,作出力图是基础.比较容易.

练习册系列答案
相关题目
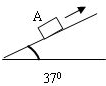 如图所示,重100N的物体A沿倾角为370的斜面向上滑动,斜面对物体A的摩擦力的大小为lON.(重力加速度g取g=10m/s2).则:
如图所示,重100N的物体A沿倾角为370的斜面向上滑动,斜面对物体A的摩擦力的大小为lON.(重力加速度g取g=10m/s2).则: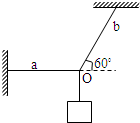 如图所示,重100N的物体,用轻质细绳a和b悬挂,绳a水平、绳b与水平方向成60°角,试回答下列问题:
如图所示,重100N的物体,用轻质细绳a和b悬挂,绳a水平、绳b与水平方向成60°角,试回答下列问题: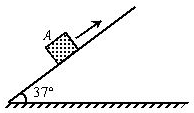 如图所示,重100N的物体A沿倾角为37°的斜面向上滑动,斜面对物体A的摩擦力的大小为10N.求:
如图所示,重100N的物体A沿倾角为37°的斜面向上滑动,斜面对物体A的摩擦力的大小为10N.求: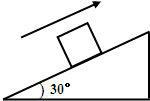 如图所示,重100N的物体A沿倾角为30°的斜面向上滑动,斜面对物体A的摩擦力的大小为l0N.求:
如图所示,重100N的物体A沿倾角为30°的斜面向上滑动,斜面对物体A的摩擦力的大小为l0N.求: 如图所示,重100N的木箱放在水平地面上,最小用40N的水平推力才能推动它,当它在水平地面上运动后,用30N的水平推力即可使木箱做匀速直线运动.由此可知,木箱与地面的最大静摩擦力为
如图所示,重100N的木箱放在水平地面上,最小用40N的水平推力才能推动它,当它在水平地面上运动后,用30N的水平推力即可使木箱做匀速直线运动.由此可知,木箱与地面的最大静摩擦力为