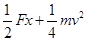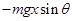题目内容
 质量为m的物块在平行于斜面的力F作用下,从固定斜面的底端A由静止开始沿斜面上滑,经B点时速率为v,此时撤去F,物块滑回斜面底端时速率也为v,斜面倾角为θ,A、B间距离为x,则( )
质量为m的物块在平行于斜面的力F作用下,从固定斜面的底端A由静止开始沿斜面上滑,经B点时速率为v,此时撤去F,物块滑回斜面底端时速率也为v,斜面倾角为θ,A、B间距离为x,则( )分析:重力做功公式WG=mgh,h是初末位置的高度差.根据动能定理研究整个过程,求解物块克服摩擦力做功.分别对上滑和下滑过程研究,求解物块克服重力做功.根据动能定理研究从撤去F到物块滑回斜面底端摩擦力做功.
解答:解:
A、根据重力做功公式WG=mgh可知,整个过程中初末位置高度差为零,则重力做功为零.故A错误.
B、对整个过程研究,根据动能定理得:Fx-Wf=0-
mv2,得到:物块克服摩擦力做功为Wf=Fx+
mv2.故B错误.
C、设上滑过程中克服重力做功为WG,则根据动能定理得:
上滑过程:Fx-WG-
Wf=0,
下滑过程:WG-
Wf=
mv2
联立两式得;WG=
(Fx+
mv2).故C错误.
D、从撤去F到物块滑回斜面底端过程,根据动能定理得:
mgxsinθ+Wf=
mv2-
mv2,得到摩擦力做功为Wf=-mgxsinθ.故D正确.
故选:D
A、根据重力做功公式WG=mgh可知,整个过程中初末位置高度差为零,则重力做功为零.故A错误.
B、对整个过程研究,根据动能定理得:Fx-Wf=0-
| 1 |
| 2 |
| 1 |
| 2 |
C、设上滑过程中克服重力做功为WG,则根据动能定理得:
上滑过程:Fx-WG-
| 1 |
| 2 |
下滑过程:WG-
| 1 |
| 2 |
| 1 |
| 2 |
联立两式得;WG=
| 1 |
| 2 |
| 1 |
| 2 |
D、从撤去F到物块滑回斜面底端过程,根据动能定理得:
mgxsinθ+Wf=
| 1 |
| 2 |
| 1 |
| 2 |
故选:D
点评:本题根据功的公式和动能定理求解重力和摩擦力做功,要灵活选择研究的过程,采用分段法和全过程两种方法结合研究.

练习册系列答案
相关题目
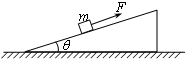 如图所示,粗糙斜面的倾角为θ.一质量为m的物块在平行于斜面向上的拉力F作用下,沿斜面向上做匀速直线运动.斜面相对水平地面保持静止不动.
如图所示,粗糙斜面的倾角为θ.一质量为m的物块在平行于斜面向上的拉力F作用下,沿斜面向上做匀速直线运动.斜面相对水平地面保持静止不动.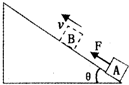 (2013?商丘二模)质量为m的物块在平行于斜面的力F作用下,从倾角为θ的固定斜面底端A由静止开始沿斜面上滑,经B点时速率为v,此时撤去F,物块滑回斜面底端时速率也为v,若A、B间距离为x,则( )
(2013?商丘二模)质量为m的物块在平行于斜面的力F作用下,从倾角为θ的固定斜面底端A由静止开始沿斜面上滑,经B点时速率为v,此时撤去F,物块滑回斜面底端时速率也为v,若A、B间距离为x,则( ) (2011?无为县模拟)质量为m的物块在平行于斜面的力F作用下,从固定斜面的底端A由静止开始沿斜面上滑,经B点时速率为v,此时撤去F,物块滑回斜面底端时速率也为v,斜面倾角为θ,A、B间距离为x,则( )
(2011?无为县模拟)质量为m的物块在平行于斜面的力F作用下,从固定斜面的底端A由静止开始沿斜面上滑,经B点时速率为v,此时撤去F,物块滑回斜面底端时速率也为v,斜面倾角为θ,A、B间距离为x,则( )

 ;
;