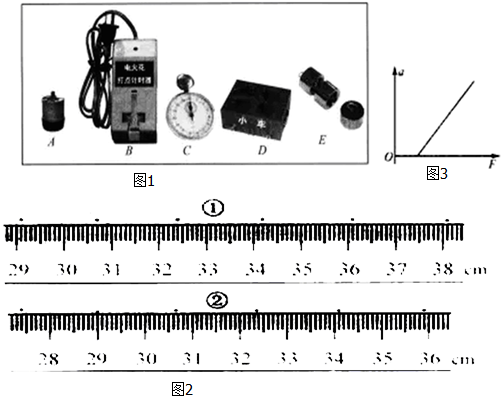
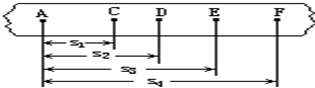
题目内容
1.某同学利用下述装置对轻质弹簧的弹性势能进行探究:一轻质弹簧放置在光滑水平桌面上,弹簧左端固定,右端与一小球接触而不固连;弹簧处于原长时,小球恰好在桌面边缘,如图(a)所示.向左推小球,使弹黄压缩一段距离后由静止释放;小球离开桌面后落到水平地面.通过测量和计算,可求得弹簧被压缩后的弹性势能.回答下列问题: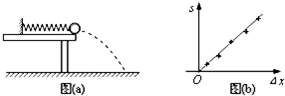
(1)本实验中可认为,弹簧被压缩后的弹性势能Ep与小球抛出时的动能Ek相等.已知重力加速度大小为g.为求得Ek,至少需要测量下列物理量中的ABC(填正确答案标号).
A.小球的质量m
B.小球抛出点到落地点的水平距离s
C.桌面到地面的高度h
D.弹簧的压缩量△x
E.弹簧原长l0
(2)用所选取的测量量和已知量表示Ek,得Ek=$\frac{mg{s}^{2}}{4h}$.
(3)图(b)中的直线是实验测量得到的s-△x图线.从理论上可推出,如果h不变,m增加,s-△x图线的斜率会减小(填“增大”、“减小”或“不变”);如果m不变,h增加,s-△x图线的斜率会增大(填“增大”、“减小”或“不变”).由图(b) 中给出的直线关系和Ek的表达式可知,Ep与△x的2次方成正比.
分析 本题的关键是通过测量小球的动能来间接测量弹簧的弹性势能,然后根据平抛规律以及动能表达式即可求出动能的表达式,从而得出结论.本题的难点在于需要知道弹簧弹性势能的表达式(取弹簧因此为零势面),然后再根据Ep=Ek即可得出结论.
解答 解(1)由平抛规律可知,由水平距离和下落高度即可求出平抛时的初速度,进而可求出物体动能,所以本实验至少需要测量小球的质量m、小球抛出点到落地点的水平距离s、桌面到地面的高度h,故选:ABC.
(2)由平抛规律应有h=$\frac{1}{2}$gt2,s=vt,又Ek=$\frac{1}{2}$mv2,联立可得Ek=$\frac{mg{s}^{2}}{4h}$.
(3)对于确定的弹簧压缩量△x而言,增大小球的质量会减小小球被弹簧加速时的加速度,从而减小小球平抛的初速度和水平位移,即h不变,m增加,相同的△x要对应更小的s,s-△x图线的斜率会减小;
对于确定的弹簧压缩量△x而言,小球的质量不变,小球平抛的初速度不变,h增加时间变长,故水平位移变大,即m不变h增加,相同的△x要对应更大的s,s-△x图线的斜率会增大.
由s的关系式和s=k△x可知,Ep与△x的二次方成正比.
故答案为:(1)ABC;(2)$\frac{mg{s}^{2}}{4h}$; (3)减小,增大,2.
点评 本题考查对轻质弹簧的弹性势能进行探究;要注意明确实验原理,根据相应规律得出表达式,然后讨论即可.

练习册系列答案
相关题目
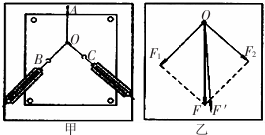
2.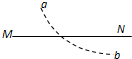 如图所示,直线MN是某电场中的一条电场线(方向未画出).虚线是一带电的粒子只在电场力的作用下,由a到b的运动轨迹,轨迹为一抛物线.下列判断正确的是( )
如图所示,直线MN是某电场中的一条电场线(方向未画出).虚线是一带电的粒子只在电场力的作用下,由a到b的运动轨迹,轨迹为一抛物线.下列判断正确的是( )
 如图所示,直线MN是某电场中的一条电场线(方向未画出).虚线是一带电的粒子只在电场力的作用下,由a到b的运动轨迹,轨迹为一抛物线.下列判断正确的是( )
如图所示,直线MN是某电场中的一条电场线(方向未画出).虚线是一带电的粒子只在电场力的作用下,由a到b的运动轨迹,轨迹为一抛物线.下列判断正确的是( )| A. | 电场线MN的方向一定是由N指向M | |
| B. | 带电粒子由a运动到b的过程中动能一定逐渐增大 | |
| C. | 带电粒子在a点的电势能小于在b点的电势能 | |
| D. | 带电粒子在a点的加速度一定大于在b点的加速度 |
20.物体做匀加速直线运动,加速度为2m/s2,那么( )
| A. | 在任意时间内,物体的末速度一定等于初速度的2倍 | |
| B. | 在任意时间内,物体的末速度一定比初速度大于2m/s | |
| C. | 在任意1s内,物体的末速度一定等于初速度的2倍 | |
| D. | 在任意1s内,物体的末速度一定比初速度大2m/s |
13.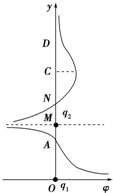 两电荷量分别为q1和q2的点电荷放在y轴上的O、M两点,若规定无穷远处的电势为零,则在两电荷连线上各点的电势φ随y变化的关系如图所示,其中A、N两点的电势均为零,ND段中的C点电势最高,则( )
两电荷量分别为q1和q2的点电荷放在y轴上的O、M两点,若规定无穷远处的电势为零,则在两电荷连线上各点的电势φ随y变化的关系如图所示,其中A、N两点的电势均为零,ND段中的C点电势最高,则( )
 两电荷量分别为q1和q2的点电荷放在y轴上的O、M两点,若规定无穷远处的电势为零,则在两电荷连线上各点的电势φ随y变化的关系如图所示,其中A、N两点的电势均为零,ND段中的C点电势最高,则( )
两电荷量分别为q1和q2的点电荷放在y轴上的O、M两点,若规定无穷远处的电势为零,则在两电荷连线上各点的电势φ随y变化的关系如图所示,其中A、N两点的电势均为零,ND段中的C点电势最高,则( )| A. | q1与q2带同种电荷 | |
| B. | A、N两点的电场强度大小为零 | |
| C. | 从N点沿y轴正方向,电场强度大小先减小后增大 | |
| D. | 将一正点电荷从N点移到D点,电场力先做负功后做正功 |
11.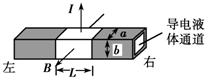 电磁泵是指处在磁场中的通电流体在电磁力作用下向一定方向流动的泵,如图所示是一电磁泵工作部分示意图,绝缘非磁性管道的横截面是长为a、宽为b的矩形,在管道内上、下管壁处各安装一个长为L的电极,通以电流I.当在垂直于管道和电流的方向加一个磁感应强度为B的匀强磁场时,电流受到的安培力就推动导电液体流动,已知导电液体稳定流动时所受阻力与流动速率成正比,即Ff=kv,则关于导电液体的流动方向和电磁泵的功率,下列说法正确的是( )
电磁泵是指处在磁场中的通电流体在电磁力作用下向一定方向流动的泵,如图所示是一电磁泵工作部分示意图,绝缘非磁性管道的横截面是长为a、宽为b的矩形,在管道内上、下管壁处各安装一个长为L的电极,通以电流I.当在垂直于管道和电流的方向加一个磁感应强度为B的匀强磁场时,电流受到的安培力就推动导电液体流动,已知导电液体稳定流动时所受阻力与流动速率成正比,即Ff=kv,则关于导电液体的流动方向和电磁泵的功率,下列说法正确的是( )
 电磁泵是指处在磁场中的通电流体在电磁力作用下向一定方向流动的泵,如图所示是一电磁泵工作部分示意图,绝缘非磁性管道的横截面是长为a、宽为b的矩形,在管道内上、下管壁处各安装一个长为L的电极,通以电流I.当在垂直于管道和电流的方向加一个磁感应强度为B的匀强磁场时,电流受到的安培力就推动导电液体流动,已知导电液体稳定流动时所受阻力与流动速率成正比,即Ff=kv,则关于导电液体的流动方向和电磁泵的功率,下列说法正确的是( )
电磁泵是指处在磁场中的通电流体在电磁力作用下向一定方向流动的泵,如图所示是一电磁泵工作部分示意图,绝缘非磁性管道的横截面是长为a、宽为b的矩形,在管道内上、下管壁处各安装一个长为L的电极,通以电流I.当在垂直于管道和电流的方向加一个磁感应强度为B的匀强磁场时,电流受到的安培力就推动导电液体流动,已知导电液体稳定流动时所受阻力与流动速率成正比,即Ff=kv,则关于导电液体的流动方向和电磁泵的功率,下列说法正确的是( )| A. | 导电液体可能向左流动 | B. | 导电液体一定向右流动 | ||
| C. | 电磁泵的功率为$\frac{{B}^{2}ab{I}^{2}}{k}$ | D. | 电磁泵的功率为$\frac{{B}^{2}{b}^{2}{I}^{2}}{k}$ |
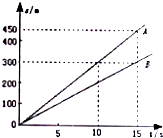 如图所示,A和B分别是甲乙两物体的s-t图象,则甲物体的速度v1=30m/s,乙物体的速度v2=15m/s,在t=15s时,甲、乙两物体相距150m.
如图所示,A和B分别是甲乙两物体的s-t图象,则甲物体的速度v1=30m/s,乙物体的速度v2=15m/s,在t=15s时,甲、乙两物体相距150m.