题目内容
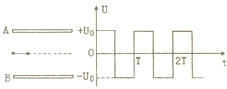 如图所示,长为L、相距为d的两平行金属板与一交流电源相连(图中未画出),有一质量为m、带电量为q的带负电的粒子以初速度Vo从板中央水平射入电场,从飞入时刻算起,A、B板间所加电压的变化规律如图所示,为了使带电粒子离开电场时速度方向恰好平行于金属板,(不计重力)问:
如图所示,长为L、相距为d的两平行金属板与一交流电源相连(图中未画出),有一质量为m、带电量为q的带负电的粒子以初速度Vo从板中央水平射入电场,从飞入时刻算起,A、B板间所加电压的变化规律如图所示,为了使带电粒子离开电场时速度方向恰好平行于金属板,(不计重力)问:(1)交变电压周期T应满足什么条件?
(2)加速电压值uo的取值范围多大?
分析:(1)带电粒子进入电场后做类平抛运动,要使带电粒子离开电场时的速度方向平行于金属板,粒子穿过电场的时间应是t=nT,粒子水平方向做匀速直线运动,由t=
求出时间,联立即可得到周期T满足的条件.
(2)在竖直方向上带电粒子通过的位移大小相等,由牛顿第二定律和运动学求出一个周期内竖直方向的位移大小h1,带电粒子在n个周期内的位移为h=nh1,要使粒子能离开电场,h应满足的条件是h≤
,即可求出交变电压的最大值U0的取值范围.
| L |
| v0 |
(2)在竖直方向上带电粒子通过的位移大小相等,由牛顿第二定律和运动学求出一个周期内竖直方向的位移大小h1,带电粒子在n个周期内的位移为h=nh1,要使粒子能离开电场,h应满足的条件是h≤
| d |
| 2 |
解答:解:(1)带电粒子穿越电场所需时间t=
①
粒子飞出电场时速度方向平行于金属板,所以:t=nT 其中n=1,2,3…②
T=
=
(n=1,2,3…) ③
(2)竖直方向上带电粒子在一个周期内的位移h1
a(
)2×2=
=
④
带电粒子在n个周期内的位移h=nh1=n
根据题意,电子能离开电场,必有 h≤
,⑥
得 n
≤
解得U0≤
将T=
=
(n=1,2,3…) 代入得
U0≤
答:(1)交变电压周期T需满足的条件是 T=
(n=1(n=1,2,3…).(2)交变电压的最大值U0的取值范围是 U0≤
(n=1,2,3…).
| L |
| v0 |
粒子飞出电场时速度方向平行于金属板,所以:t=nT 其中n=1,2,3…②
T=
| t |
| n |
| L |
| nv0 |
(2)竖直方向上带电粒子在一个周期内的位移h1
| 1 |
| 2 |
| T |
| 2 |
| qU0 |
| md |
| T2 |
| 4 |
| qU0T2 |
| 4md |
带电粒子在n个周期内的位移h=nh1=n
| qU0T2 |
| 4md |
根据题意,电子能离开电场,必有 h≤
| d |
| 2 |
得 n
| qU0T2 |
| 4md |
| d |
| 2 |
解得U0≤
| 2d2m |
| qT2 |
| 1 |
| n |
将T=
| t |
| n |
| L |
| nv0 |
U0≤
2nmd2
| ||
| qL2 |
答:(1)交变电压周期T需满足的条件是 T=
| L |
| nv0 |
2nmd2
| ||
| qL2 |
点评:本题考查带电粒子在电场中的偏转,理清粒子的运动规律,结合运动学公式和牛顿第二定律进行求解.

练习册系列答案
 名师伴你成长课时同步学练测系列答案
名师伴你成长课时同步学练测系列答案
相关题目
 如图所示,宽度为L=0.4m的金属框架竖直固定在绝缘地面上,框架的上端接有一特殊的电子元件,如果将其作用等效成一个电阻,则其阻值与其两端所加的电压成正比,即等效电阻R=kU,式中k=2.0Ω/V.框架上有一质量为m=1.0kg的金属棒水平放置,金属棒与框架接触良好无摩擦,离地高为h=4.0m,磁感应强度为B=10.0T的匀强磁场与框架平面相垂直.将金属棒由静止释放,棒沿框架向下运动.不计金属棒电阻,g=10m/s2,问:
如图所示,宽度为L=0.4m的金属框架竖直固定在绝缘地面上,框架的上端接有一特殊的电子元件,如果将其作用等效成一个电阻,则其阻值与其两端所加的电压成正比,即等效电阻R=kU,式中k=2.0Ω/V.框架上有一质量为m=1.0kg的金属棒水平放置,金属棒与框架接触良好无摩擦,离地高为h=4.0m,磁感应强度为B=10.0T的匀强磁场与框架平面相垂直.将金属棒由静止释放,棒沿框架向下运动.不计金属棒电阻,g=10m/s2,问: 如图所示,宽度为L的金属框架竖直固定在绝缘地面上,框架的上端接有一特殊的电子元件,如果将其作用等效成一个电阻,则其阻值与其两端所加的电压成正比,即等效电阻R=kU,式中k为恒量.框架上有一质量为m的金属棒水平放置,金属棒与框架接触良好无摩擦,离地高为h,磁感应强度为B的匀强磁场与框架平面相垂直.将金属棒由静止释放,棒沿框架向下运动.不计金属棒电阻,问:
如图所示,宽度为L的金属框架竖直固定在绝缘地面上,框架的上端接有一特殊的电子元件,如果将其作用等效成一个电阻,则其阻值与其两端所加的电压成正比,即等效电阻R=kU,式中k为恒量.框架上有一质量为m的金属棒水平放置,金属棒与框架接触良好无摩擦,离地高为h,磁感应强度为B的匀强磁场与框架平面相垂直.将金属棒由静止释放,棒沿框架向下运动.不计金属棒电阻,问: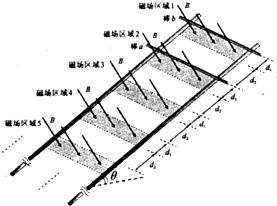 如图所示,间距为L的两条足够长的平行金属导轨与水平面的夹角为θ,导轨光滑且电阻忽略不计.场强为B的条形匀强磁场方向与导轨平面垂直,磁场区域的宽度为d1,间距为d2.两根质量均为m、有效电阻均为R的导体棒a和b放在导轨上,并与导轨垂直. (设重力加速度为g)
如图所示,间距为L的两条足够长的平行金属导轨与水平面的夹角为θ,导轨光滑且电阻忽略不计.场强为B的条形匀强磁场方向与导轨平面垂直,磁场区域的宽度为d1,间距为d2.两根质量均为m、有效电阻均为R的导体棒a和b放在导轨上,并与导轨垂直. (设重力加速度为g)  (08年江苏卷)(16分)如图所示,间距为L的两条足够长的平行金属导轨与水平面的夹角为θ,导轨光滑且电阻忽略不计。场强为B的条形匀强磁场方向与导轨平面垂直,磁场区域的宽度为d1,间距为d2。两根质量均为m、有效电阻均为R的导体棒a和b放在导轨上,并与导轨垂直。(设重力加速度为g)
(08年江苏卷)(16分)如图所示,间距为L的两条足够长的平行金属导轨与水平面的夹角为θ,导轨光滑且电阻忽略不计。场强为B的条形匀强磁场方向与导轨平面垂直,磁场区域的宽度为d1,间距为d2。两根质量均为m、有效电阻均为R的导体棒a和b放在导轨上,并与导轨垂直。(设重力加速度为g)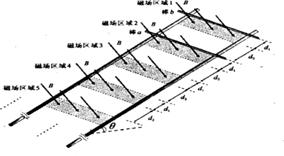 如图所示,间距为L的两条足够长的平行金属导轨与水平面的夹角为θ,导轨光滑且电阻忽略不计.场强为B的条形匀强磁场方向与导轨平面垂直,磁场区域的宽度为d1,间距为d2.两根质量均为m、有效电阻均为R的导体棒a和b放在导轨上,并与导轨垂直. (设重力加速度为g)
如图所示,间距为L的两条足够长的平行金属导轨与水平面的夹角为θ,导轨光滑且电阻忽略不计.场强为B的条形匀强磁场方向与导轨平面垂直,磁场区域的宽度为d1,间距为d2.两根质量均为m、有效电阻均为R的导体棒a和b放在导轨上,并与导轨垂直. (设重力加速度为g)