题目内容
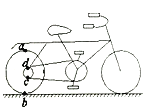
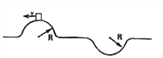
【题目】如下图所示，一质量为M的赛车，在某次比赛中要以恒定的速率通过一段凹凸起伏的圆弧形路面，若圆弧半径都是R，汽车在最高点对路面的压力为零，则下列说法正确的是
A. 在凸起的圆弧路面的顶部，汽车处于超重状态
B. 在凹下的圆弧路面的底部，汽车对路面的压力为2Mg
C. 在经过凸起的圆弧路面的顶部后，汽车将做平抛运动，落地点到最高点得水平距离为2R
D. 汽车在弧形轨道上运动的过程中向心力保持不变
【答案】B
【解析】在凸起的圆弧路面的顶部，汽车在最高点对路面的压力为零，重力提供向心力，向心加速度的方向向下，汽车处于失重状态．故A错误；汽车在最高点对路面的压力为零，重力提供向心力根据牛顿第二定律，有：Mg=M
；则速率为：
；在凹下的圆弧路面的底部，重力和支持力的合力提供向心力，根据牛顿第二定律，有：N-Mg=M；速率恒为；
解得：N=2Mg，根据牛顿第三定律，汽车对路面的压力为2Mg，故B正确；由于在凸起的圆弧路面的顶部，支持力为零，故此后车将做平抛运动，平抛运动的时间：
，所以平抛运动的水平位移：x=vt=
R．故C错误；由于速率恒为，故向心力大小等于：Fn=M=Mg，但方向不断变化．故D错误；故选B.
练习册系列答案
相关题目
