题目内容
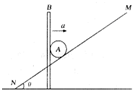
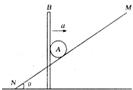如图所示．斜面MN的倾角θ=37°，斜面上有一质量为m的物体A，B是一带竖直推板的直杆，其质量为2m．现使直杆B以水平加速度a=0.4g 向右运动，从而推动物体A沿斜面向上运动．物体A与直杆B及斜面之间的摩擦均不计，直杆B始终保持竖直状态，sin37°=0.6，cos37°=0.8．求此时：（l）物体A的加速度大小．（2）直杆B对物体A的推力大小．
解：（1）A的合加速度方向沿斜面向上，
其水平向右的分加速度和B的加速度相同，有：
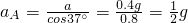
（2）对A受力分析，由牛顿第二定律得：
Fcos37°-mgsin37°=maA
代入数据解得：
F=
．
答：（1）物体A的加速度大小为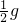
．
（2）直杆B对物体A的推力大小为．
分析：（1）A的合加速度方向沿斜面向上，其水平向右的分加速度和B的加速度相同，根据几何关系即可求解；
（2）对A运用牛顿第二定律去求直杆 B 对物体 A 的推力；
点评：本题要注意A和B的加速度之间的关系，再结合牛顿第二定律去解题，难度适中．
其水平向右的分加速度和B的加速度相同，有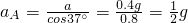：（2）对A受力分析，由牛顿第二定律得：
Fcos37°-mgsin37°=maA
代入数据解得：
F=
．答：（1）物体A的加速度大小为
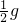．（2）直杆B对物体A的推力大小为
．分析：（1）A的合加速度方向沿斜面向上，其水平向右的分加速度和B的加速度相同，根据几何关系即可求解；
（2）对A运用牛顿第二定律去求直杆 B 对物体 A 的推力；
点评：本题要注意A和B的加速度之间的关系，再结合牛顿第二定律去解题，难度适中．
练习册系列答案
相关题目
如图所示．斜面MN的倾角θ=37°，斜面上有一质量为m的物体A，B是一带竖直推板的直杆，其质量为2m．现使直杆B以水平加速度a=0.4g 向右运动，从而推动物体A沿斜面向上运动．物体A与直杆B及斜面之间的摩擦均不计，直杆B始终保持竖直状态，sin37°=0.6，cos37°=0.8．求此时：（l）物体A的加速度大小．（2）直杆B对物体A的推力大小．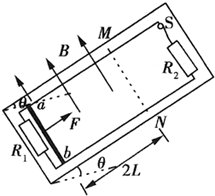
如图所示，相互平行的光滑金属导轨固定在倾角为θ=30°的绝缘斜面上，相距为L，导轨下端连接一个定值电阻R1，上端通过开关S（S是闭合的）连接一个定值电阻R2．导体棒ab放在导轨上靠近下端的位置，与导轨垂直并接触良好．在导轨平面上虚线MN以下的区域内，存在着垂直穿过斜面向上的匀强磁场．现对导体棒施加平行导轨向上的恒定拉力F，使它沿导轨先向上加速运动，在到达虚线MN之前，导体棒已经开始做匀速运动，速度大小为
