题目内容
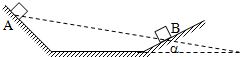（2006?宝山区模拟）如图所示，一带正电物体从斜面的A处由静止开始滑下，经过一水平面后又滑上右边的斜面并停留在B处，AB连线与水平面成α角，若在整个空间加上竖直向下的电场，则该物体从A点由静止滑下，到达右边的斜面并停留在C处（图中未标出），AC连线与水平面夹角为β，若接触面处动摩擦因素处处相等，斜面与水平面接触处是小圆弧，则α、β的关系是α等于
等于
β（选填“大于”、“小于”或“等于”）．分析：本题的关键是对全过程列出动能定理方程，然后根据摩擦力做功的公式得出动摩擦因数μ与AB连线与水平面θ的关系，同理列出空间加上竖直向下的电场后全过程动能定理表达式，整理可得结论．
解答：解：设斜面倾角为θ，斜面长为L，物体在斜面上下滑过程中克服阻力做的功为
=μmgcosθ．L=μm
，则全过程由动能定理应有mg△
-
=0，即mg
=μm
，即μ=
=tanα，同理，加入竖直向下的电场后，对全过程由动能定理有（mg+gE）
-μ（mg+gE）
=0，其中
=
，
整理可得sinβ=μcosβ，即μ=tanβ
，比较可得β=α
故答案为：等于．
| W | 克 |
| gL | 水平 |
| h | AB |
| W | 克 |
| ABsinα |
| gABcosα |
| sinα |
| cosα |
| △h | ′ |
| ACcosβ |
| △h | ′ |
| ACsinβ |
整理可得sinβ=μcosβ，即μ=tanβ
，比较可得β=α
故答案为：等于．
点评：掌握斜面上运动过程中摩擦力做功的特点，对多运动过程应用全过程动能定理解决．
练习册系列答案
相关题目
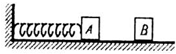（2006?宝山区模拟）一轻弹簧一端系在墙上，自由伸长时，右端正好处在B处，今将一质量为m的小物体靠着弹簧，将弹簧压缩到A处，然后释放，如图所示．小物体能在水平面上运动到C点静止，AC距离为s；如将小物体系在弹簧上，在A由静止释放，则小物体将向右运动，或来回运动后最终停止，设小物体通过的总路程为L，则下列选项可能的是（ ）
（2006?宝山区模拟）如图所示，一对男女杂技演员荡秋千（秋千质量不计），当秋千悬绳处于水平位置时秋千从A点由静止出发绕悬点O下摆，当摆到最低点B时，女演员在极短时间内将男演员沿水平方向推出，此推出瞬间，男女演员总机械能增为原来的3倍（以B点所在的水平面为重力势能的零势能面），然后女演员刚好能回到A处．已知男女演员质量之比为2：1，秋千的悬绳长为L，C点比O点低5L．求男演员落地点C距O点的水平距离s．
（2006?宝山区模拟）如图是一个应用某种逻辑电路制作的简单车门报警电路图．图中的两个按钮开关分别装在汽车的两道门上．只要其中任何一个开关处于开路状态，发光二极管就发光．请你根据报警装置的要求，在电路图的虚线框内画出门电路的符号．
（2006?宝山区模拟）如图所示，质点O在垂直x轴方向上做简谐振动，形成了沿x轴传播的横波．在t=0时刻质点O开始向上运动，经0.2s第一次形成图示波形，由此判断在t=2.5s时刻，质点A、B的运动情况是（ ）