��Ŀ����
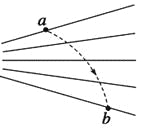
����Ŀ����ͼ��ʾ���⻬��Բ������İ뾶ΪR��OAΪˮƽ�뾶��BCΪ��ֱֱ�����⻬��Բ�������ֲ�ˮƽ����CM������C�㣬��ˮƽ��������һ�ᵯ�ɣ���һ�˹̶�����ֱǽ�ϣ���һ��ǡ��λ�ڻ�����ĩ��C��(��ʱ���ɴ�����Ȼ״̬)���ڵ����Ҷ˷���һ����Ϊm�����(����Ϊ�ʵ�)�����������ƶ����ѹ�����ɣ�ʹ���ɵĵ�������Ϊ![]() ����ȥ�����ͷ���飬��鱻���ɵ���ȥ��ǡ�ܵ���A�㡣��֪�����ˮƽ������Ķ�Ħ������Ϊ�����������ٶȴ�СΪg����
����ȥ�����ͷ���飬��鱻���ɵ���ȥ��ǡ�ܵ���A�㡣��֪�����ˮƽ������Ķ�Ħ������Ϊ�����������ٶȴ�СΪg����

(1)����뿪���ɸս����Բ���ʱ�Թ����ѹ����СFN��
(2)��ȥ����ʱ���ɵ�ѹ����d
���𰸡���1��3mg��2��![]()
��������
��1�����ݻ�е���غ㶨�����С����˶���C����ٶȣ�����ţ�ٵڶ��������C���֧������С������ţ�ٵ������ɿɵ����Թ����ѹ������2���������غ㶨��������ɵ�ѹ����d��
��1������֪����鱻���ɵ���ȥ��ǡ�ܵ���A�㣬���C��A���ɻ�е���غ�ã�![]()
��C�㣬����ţ�ٵڶ����ɵã�![]()
������ã�![]()
����ţ�ٵ������ɿ�֪����뿪���ɸս����Բ���ʱ�Թ����ѹ����СΪ3mg
��2�����ɴ�ѹ������̿�ʼ������鱻���뵯�ɵĹ�����
���������غ�ã�![]()
��ã�![]()

 ����ȫ���ִʾ��ƪ��ϵ�д�
����ȫ���ִʾ��ƪ��ϵ�д� �����߿����ϵ�д�
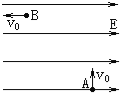
�����߿����ϵ�д�����Ŀ��ijѧϰС��������ͼ��ʾ��ʵ��װ��̽�����߹���Ȧ�и�Ӧ�����ķ���

��1�����ڴ��ĸ�С����ɱ���ʱ©����һ���֣����������ֺ����������ⲿ�֣�������S�����´����߹��Ϸ���ֱ������̣����ֵ�����ָ������ƫת����֪�������ҽ��������������ʱ����ָ������ƫת���������________������________��
Bԭ���� | ���� | I���������� | B������ | |
N������ | ���� | ���� | ��ʱ�� | ���� |
S������ | ���� | ���� | �� | �� |
N����� | ���� | ��С | ˳ʱ�� | ���� |
S����� | ���� | ��С | ��ʱ�� | ���� |
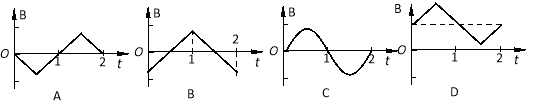
��2����ʵ��ɵô�ͨ���仯������ԭ�ų�Bԭ����Ӧ�����Ĵų�B����������֮��Ĺ�ϵ��________��