题目内容
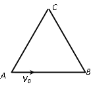
【题目】一质量m、带电q的粒子以速度v0从A点沿等边三角形ABC的AB方向射入强度为B的垂直于纸面的圆形匀强磁场区域中，要使该粒子飞出磁场后沿BC射出，求圆形磁场区域的最小面积。
【答案】
【解析】
根据带电粒子在磁场中运动时,洛仑兹力提供向心力即可求得半径,由几何知识求出粒子转过的圆心角,以粒子在磁场区入射点和出射点的弦长为半径的圆,面积最小,求出磁场的半径,然后求出磁场的最小面积
带电粒子在磁场中运动时,洛仑兹力提供向心力,由牛顿第二定律得:
,
计算得出
,
根据题意粒子以速度v0从A点沿等边三角形ABC的AB方向射入强度为B的垂直于纸面的圆形匀强磁场区域中，要使该粒子飞出磁场后沿BC射出，则粒子在磁场中转过的圆心角为
以粒子入射点与出射点连线为半径的圆面积最小,由几何知识得
:,
磁场半径:
,
磁场的最小面积
练习册系列答案
口算能手系列答案
相关题目
