题目内容
14.质量为m的物体静止在水平面上,物体与水平面的动摩擦因素为μ,有一水平恒力F作用于该物体,使物体加速前进,经过时间t1撤去此力,试求:物体运动的总时间.分析 根据牛顿第二定律求出匀加速直线运动以及撤去拉力后匀减速直线运动的加速度,结合速度时间公式求出时间.
解答 解:匀加速直线运动的加速度a=$\frac{F-μmg}{m}=\frac{F}{m}-μg$,匀加速直线运动的末速度$v=at=\frac{F{t}_{1}}{m}-μg{t}_{1}$.
匀减速直线运动的加速度大小$a′=\frac{f}{m}=μg$.
则匀减速运动的时间t′=$\frac{v}{a′}=\frac{F{t}_{1}}{μmg}-{t}_{1}$.
则总时间${t}_{总}={t}_{1}+t′=\frac{F{t}_{1}}{μmg}$.
答:物体运动的总时间是$\frac{{F{t_1}}}{μmg}$.
点评 本题考查牛顿第二定律和运动学公式的综合运用,知道加速度是联系力学和运动学的桥梁.本题也可以通过动量定理进行求解.

练习册系列答案
相关题目
5.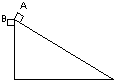 如图所示,质量相同的两物体处于同一高度,A沿固定在地面上的光滑斜面下滑,B自由下落,最后到达同一水平面,则( )
如图所示,质量相同的两物体处于同一高度,A沿固定在地面上的光滑斜面下滑,B自由下落,最后到达同一水平面,则( )
 如图所示,质量相同的两物体处于同一高度,A沿固定在地面上的光滑斜面下滑,B自由下落,最后到达同一水平面,则( )
如图所示,质量相同的两物体处于同一高度,A沿固定在地面上的光滑斜面下滑,B自由下落,最后到达同一水平面,则( )| A. | 重力对两物体做功相同 | |
| B. | 重力的平均功率相同 | |
| C. | 到达底端时重力的瞬时功率PA大于PB | |
| D. | 到达底端时两物体的速度相同 |
2. 如图所示,一列简谐横波沿x轴正方向传播,t=0时,该波传播到x轴上的质点B处,质点A在负的最大位移处.在t=0.6s时,质点A第二次通过平衡位置,则( )
如图所示,一列简谐横波沿x轴正方向传播,t=0时,该波传播到x轴上的质点B处,质点A在负的最大位移处.在t=0.6s时,质点A第二次通过平衡位置,则( )
 如图所示,一列简谐横波沿x轴正方向传播,t=0时,该波传播到x轴上的质点B处,质点A在负的最大位移处.在t=0.6s时,质点A第二次通过平衡位置,则( )
如图所示,一列简谐横波沿x轴正方向传播,t=0时,该波传播到x轴上的质点B处,质点A在负的最大位移处.在t=0.6s时,质点A第二次通过平衡位置,则( )| A. | 该波的周期为1.2s | B. | 该波的波速等于5m/s | ||
| C. | t=0.6s时,质点B在正的最大位移处 | D. | t=0.6s时,质点C在正的最大位移处 |
9.下列说法中正确的是( )
| A. | 物体受到的冲量越大,则它的动量一定越大 | |
| B. | 物体受到的冲量越大,则它的动量变化量越大 | |
| C. | 物体动量变化的方向一定与物体所受合外力的冲量方向相同 | |
| D. | 物体沿斜面下滑,斜面对物体的支持力对物体不做功,支持力的冲量也为零 |
19. 如图所示是电子射线管示意图.接通电源后,电子射线由阴极沿x轴方向射出,在荧光屏上会看到一条亮线.要使荧光屏上的亮线向下(z轴负方向)偏转,在下列措施中可采用的是( )
如图所示是电子射线管示意图.接通电源后,电子射线由阴极沿x轴方向射出,在荧光屏上会看到一条亮线.要使荧光屏上的亮线向下(z轴负方向)偏转,在下列措施中可采用的是( )
 如图所示是电子射线管示意图.接通电源后,电子射线由阴极沿x轴方向射出,在荧光屏上会看到一条亮线.要使荧光屏上的亮线向下(z轴负方向)偏转,在下列措施中可采用的是( )
如图所示是电子射线管示意图.接通电源后,电子射线由阴极沿x轴方向射出,在荧光屏上会看到一条亮线.要使荧光屏上的亮线向下(z轴负方向)偏转,在下列措施中可采用的是( )| A. | 加一磁场,磁场方向沿z轴负方向 | B. | 加一磁场,磁场方向沿y轴正方向 | ||
| C. | 加一电场,电场方向沿z轴负方向 | D. | 加一电场,电场方向沿y轴正方向 |
3. 如图甲所示,理想变压器原、副线圈的匝数比为4:1,电压表和电流表均为理想交流电表,原线圈接如图乙所示的正弦交流电,图中R为NTC型热敏电阻(阻值随温度的升高而减小),R1为定值电阻,下列说法正确的是( )
如图甲所示,理想变压器原、副线圈的匝数比为4:1,电压表和电流表均为理想交流电表,原线圈接如图乙所示的正弦交流电,图中R为NTC型热敏电阻(阻值随温度的升高而减小),R1为定值电阻,下列说法正确的是( )
 如图甲所示,理想变压器原、副线圈的匝数比为4:1,电压表和电流表均为理想交流电表,原线圈接如图乙所示的正弦交流电,图中R为NTC型热敏电阻(阻值随温度的升高而减小),R1为定值电阻,下列说法正确的是( )
如图甲所示,理想变压器原、副线圈的匝数比为4:1,电压表和电流表均为理想交流电表,原线圈接如图乙所示的正弦交流电,图中R为NTC型热敏电阻(阻值随温度的升高而减小),R1为定值电阻,下列说法正确的是( )| A. | 交流电压M的表达式u=36$\sqrt{2}$sin50πt(V) | |
| B. | Rt处温度升高时,电流表A的示数变大,电压表V2示数减小 | |
| C. | 变压器原、副线圈中的电流之比随Rt处温度的变化而变化 | |
| D. | Rt处温度升高时,变压器原线圈的输入功率变大 |