��Ŀ����
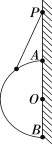
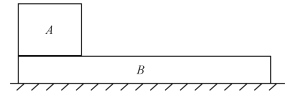
����Ŀ����ͼ��ʾ��һ��С����ֹ�ڹ⻬ˮƽ�����ϣ�С���Ϲ̶��Ű뾶ΪR��![]() �⻬Բ�������С�������������ΪM�������ˮƽ������Ϊm����龲����Բ������ˣ������Կ����ʵ㣬��һ����Ϊm0���ӵ������ٶ�Ϊv0ˮƽ����������飬���������У��ӵ��������ʱ�伫�̡���
�⻬Բ�������С�������������ΪM�������ˮƽ������Ϊm����龲����Բ������ˣ������Կ����ʵ㣬��һ����Ϊm0���ӵ������ٶ�Ϊv0ˮƽ����������飬���������У��ӵ��������ʱ�伫�̡���

��1���ӵ���������˲�䣬���Թ����ѹ����С��
��2�������������ߵ�ʱ��С�����ٶȣ�
��3�����Ժ��˶��Ĺ����У�С��������ٶȡ�
���𰸡���1�� ;��2��
;��2��![]() ;��3��
;��3��![]()
��������
��1���ӵ�����ľ�����ʱ�伫�̣��ù������ӵ���ľ��ϵͳ�����غ㣬�ɵã�
m0v0����m0+m��v1
�ӵ�����ľ���˲�䣬���������ɵã�FN����m0+m��g����m0+m��![]()
��ţ�ٵ������ɵã�![]()
��2���������֪�������������ߵ�ʱ�������С�����ٶ���ͬ���������̣�ϵͳˮƽ�������غ㣺
��m0+m��v1����m0+m+M��v
��ô�ʱС�����ٶ�Ϊ��![]()
��3������鷵�ع����͵�ʱ��С�����ٶ����ľ���ع����ʼ�˶�������ص������͵㣬ˮƽ�������غ㣺
��m0+m��v1����m0+m��v2+Mvmax
��������ϵͳ��е���غ㣺![]()
��������ʽ�ɽ�ã�С��������ٶȣ�vmax![]()

��ϰ��ϵ�д�
 ��ʦָ����ĩ��̾�ϵ�д�
��ʦָ����ĩ��̾�ϵ�д� �����ܿ����ϵ�д�
�����ܿ����ϵ�д�
�����Ŀ