题目内容
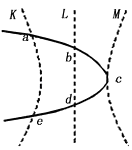
【题目】用如图所示的装置验证动量守恒定律.先将质量为m1的小球A从斜槽轨道上端无初速释放,经轨道末端水平抛出,经时间t落在水平地面上的P点.然后在轨道末端放置质量为m2的小球B(两球形状相同,m1>m2),将A球从同一位置无初速释放,与球B碰撞后,两球分别落在地面上的M点和N点.轨道末端的重锤线指向地面上的O点,测得OM=a,OP=b,ON=c,忽略小球的半径.求: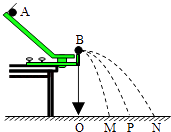
(1)与B球碰撞前瞬间A球的动量;
(2)A与B碰撞过程中,动量守恒的表达式.
【答案】
(1)解:碰撞前A的速度: ![]()
与B球碰撞前瞬间A球的动量: ![]()
答:与B球碰撞前瞬间A球的动量是 ![]() ;
;
(2)解:要验证动量守恒定律定律,即验证:m1v1=m1v2+m2v3,
小球离开轨道后做平抛运动,它们抛出点的高度相等,在空中的运动时间t相等,上式两边同时乘以t得:m1v1t=m1v2t+m2v3t,
得:m1OP=m1OM+m2ON,
将OM=a,OP=b,ON=c代入可得:m1b=m1a+m2c
答:A与B碰撞过程中,动量守恒的表达式是m1b=m1a+m2c
【解析】由动量的公式计算出与B球碰撞前瞬间A球的动量;由动量守恒定律求出需要验证的表达式.

练习册系列答案
相关题目