题目内容
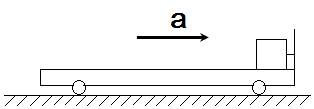
 如图所示,一个小滑块(可视为质点)通过长度不计的短绳拴在小车的板壁上,小滑块与小车底板无摩擦,小车由静止开始向右作匀加速运动,经3s绳断裂(设绳断裂后小车运动的加速度不变),又经一段时间t小滑块从小车尾部掉下来.在t这段时间内,已知小滑块相对于小车在头2s内滑行2m,最后2s内滑行5m.求:
如图所示,一个小滑块(可视为质点)通过长度不计的短绳拴在小车的板壁上,小滑块与小车底板无摩擦,小车由静止开始向右作匀加速运动,经3s绳断裂(设绳断裂后小车运动的加速度不变),又经一段时间t小滑块从小车尾部掉下来.在t这段时间内,已知小滑块相对于小车在头2s内滑行2m,最后2s内滑行5m.求:(1)小车底板长是多少?
(2)从小车开始运动到小滑块离开车尾,小滑块相对于地面移动的距离是多少?
分析:(1)绳子断裂前,物块和小车一起做匀加速运动,绳子断裂后,小车以不变的加速度做匀加速运动,物块做匀速直线运动,根据滑块相对小车前2s内滑行了2m,求出绳子断裂时的速度,再根据后2s内滑行了5m,求出后3s内的初速度,从而确定滑块在小车上运动的总时间,分别求出小车和木块的位移,两者位移之差为小车的板长.
(2)滑块相对于地面做匀速直线运动,根据s滑=v1t总求出相对于地面移动的距离.
(2)滑块相对于地面做匀速直线运动,根据s滑=v1t总求出相对于地面移动的距离.
解答:解:(1)设小车的加速度为a,以地面为参考系,绳断时为计时起点和坐标原点,则滑块 以v=3a做匀速运动,
以v=3a做匀速运动,
车以v0=3a做加速度为a的匀加速运动.头2s内:x车=v0t+
at2=8a ①
x物=v0t=6a ②
根据题意:x车-x物=2 ③
联系①②③得:
a=1m/s2
设滑块离开车尾时小车速度为v',最后2s内:
x车′=v′2-
a×22=2v′-2④
x物′=3a×2=6 ⑤
又:x车′-x物′=5 ⑥
联立④⑤⑥得:v′=6.5m/s
滑块在小车上滑行时间t=
=3.5s
小车底板长L=
at2=6.125m
(2)小滑块相对于地面移动的距离
x=
a×32+vt=15m
答:(1)小车底板长是6.125m.
(2)从小车开始运动到小滑块离开车尾,小滑块相对于地面移动的距离是多少15m.
 以v=3a做匀速运动,
以v=3a做匀速运动,车以v0=3a做加速度为a的匀加速运动.头2s内:x车=v0t+
| 1 |
| 2 |
x物=v0t=6a ②
根据题意:x车-x物=2 ③
联系①②③得:
a=1m/s2
设滑块离开车尾时小车速度为v',最后2s内:
x车′=v′2-
| 1 |
| 2 |
x物′=3a×2=6 ⑤
又:x车′-x物′=5 ⑥
联立④⑤⑥得:v′=6.5m/s
滑块在小车上滑行时间t=
| v′-v0 |
| a |
小车底板长L=
| 1 |
| 2 |
(2)小滑块相对于地面移动的距离
x=
| 1 |
| 2 |
答:(1)小车底板长是6.125m.
(2)从小车开始运动到小滑块离开车尾,小滑块相对于地面移动的距离是多少15m.
点评:解决本题的关键知道绳子断裂后,小车以不变的加速度做匀加速运动,物块做匀速直线运动.再根据匀变速直线运动的公式进行求解.

练习册系列答案
相关题目