��Ŀ����
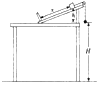
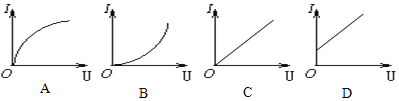
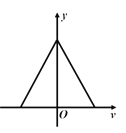
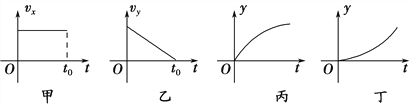
����Ŀ����ͼ����ʾ������ƽ�е�����L��1m���������37�㣬�����������һ��ֵR��10���Ķ�ֵ���裬����������m��50g������r��10���ĵ����MN�̶�����������d1������б�������ڿռ�����Ŵ�ֱ�ڹ��ƽ�����µĴų����Ÿ�Ӧǿ��B�ı仯������ͼ����ʾ����t��1sʱ��ȥ������֮�����������͵�PQλ�ú���ˮƽ�����ˮƽ����ų������������ͣ�ھ���PQ��λ��d3��0.4m������֪����͵����֮�们��Ħ����������Ϊ0.5�����������PQ֮ǰ�Ѿ��ﵽ����ٶȣ�����ת�䴦������ʧ��d1��1m��d2��4m��d3��0.4m����
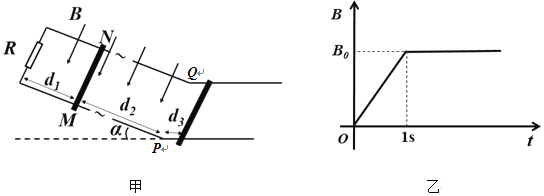
��1���ж�0��1s��ͨ�������MN�ĵ�������
��2���ų�ǿ��B0�Ĵ�С��
��3�����������ж�ֵ�����������Ľ�����Q��
���𰸡�1��0��1s��ͨ�����������������Mָ��N����2��1T����3��0.175J��
��������
��1��������ζ��ɿɵã���Ӧ����������Mָ��N��
��2������˽��뵽ˮƽ���֮�����ȼ���ֱ���˶������ٶȴ�СΪa����g
����λ���ٶȹ�ϵ�ɵã�v2��2ad3��
�õ���v��2m/s
�����������б�������͵���ٶ�Ϊ2m/s��
����ƽ�������ɵã�mgsin������mgcos��+B0I2L��
���ݱպϵ�·��ŷķ���ɿɵã�I2![]()
������ã�B0��1T��
��3��0��1s�ڲ����ĸ�Ӧ�綯��Ϊ��E1![]() d1��
d1��
���ݱպϵ�·��ŷķ���ɿɵõ���ǿ��Ϊ��I1![]()
�����Ľ�����Ϊ��Q1��I12Rt
������ã�Q1��0.025J��
1s֮����͵�֮ǰ�����ݹ��ܹ�ϵ�ɵã�Q����mgd2sin������mgcos��d2![]()
���Q����0.3J
�˹�����R�ϲ����Ľ�����Ϊ��Q2![]() Q����0.15J��
Q����0.15J��
�������̶�ֵ��������Ľ�����Ϊ��Q��Q1+Q2��0.175J��