题目内容
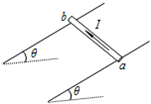
如图所示,AOB为水平放置的光滑杆,夹角∠AOB等于60°,杆上分别套着两个质量都是m的小环,两环由可伸缩的轻质弹性绳连接,若在绳的中点施以沿∠AOB 的角平分线水平向右的拉力F,缓慢地拉绳,待两环受力达到平衡时,绳对环的拉力T跟F的关系是( )
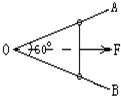
| A.T=F | B.T>F | C.T<F | D.T=Fsin30° |

据题,光滑杆AOB水平放置,两环竖直方向所受的重力与杆对两环的支持力各自平衡,不再分析.以两环及弹性轻绳整体为研究对象,分析水平方向整体受力情况:
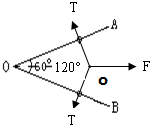
在水平面内,对两环都受到杆的弹力N和轻绳的拉力T,由二力平衡原理得知,N与T大小相等,方向相反,而N与杆垂直,则平衡时,轻绳的拉力必定与杆垂直,所以水平面整体的受力图如图.由几何知识得到∠TOT=120°,根据对称性,由平衡条件得到T=F.选项A正确,BCD错误.
故选A

在水平面内,对两环都受到杆的弹力N和轻绳的拉力T,由二力平衡原理得知,N与T大小相等,方向相反,而N与杆垂直,则平衡时,轻绳的拉力必定与杆垂直,所以水平面整体的受力图如图.由几何知识得到∠TOT=120°,根据对称性,由平衡条件得到T=F.选项A正确,BCD错误.
故选A

练习册系列答案
相关题目