题目内容
7.一段凹槽A内侧之间的距离为l,倒扣在水平长木板C上,槽内有一个可看成质点的小物块B,它紧贴槽A内的左侧,如图所示,木板位于光滑水平的桌面上,槽与木板间的摩擦不计,小物块与木板间的动摩擦因数为μ.B、C二者质量相等,原来都静止,现使B以大小为v0的初速度向右运动,已知v0<$\sqrt{2μgl}$.求:
(1)在A、B发生碰撞前,B、C能否达到共同速度?
(2)从B开始运动到A、B发生碰撞的时间内,木板C运动的位移?
分析 (1)槽与木板间的摩擦不计,因此B在C上滑动时,槽A不动,B向右匀减速、C向右匀加速.根据动能定理求出速度相等时B的位移,判断出是否与A发生碰撞.
(2)B、C达到共同速度后,B、C一起匀速运动,然后B与A的右端发生碰撞,根据动能定理求出C的位移.
解答 解:(1)槽与木板间的摩擦不计,因此B在C上滑动时,槽A不动,B向右匀减速、C向右匀加速.
由a=$\frac{F}{m}$,因为B、C二者质量相等,设为m,故它们的加速度大小相等.
用v1表示它们的共同速度,
则对C:v1=at ①
则对B:v1=v0-at ②
设B、C达到共同速度时,B移动的位移为x1,对B由动能定理得:μmgx1=$\frac{1}{2}$mv02-$\frac{1}{2}$mv12 ③
解①②③得:x1=$\frac{3{v}_{{0}^{2}}}{8μg}$ ④
根据题设条件v0<$\sqrt{2μgl}$,
可解得:x1=$\frac{3}{4}$l<l⑤
可见,B、C达到共同速度v1时,B尚未与A发生碰撞.
(2)B、C达到共同速度后,B、C一起匀速运动(l-x1)距离,B才能与A的右端发生碰撞.设C的速度由0增到v1的过程中,C前进的位移为x2.对C由动能定理得
μmgx2=$\frac{1}{2}$mv12⑥
解得x2=$\frac{{{v}_{0}}^{2}}{8μg}$⑦
从B开始运动到A、B发生碰撞的时间内,木板C运动的位移
x=x2+(l-x1)⑧
联立④⑦⑧解得:x=l-$\frac{{{v}_{0}}^{2}}{4μg}$.
答:(1)已达到共同速度
(2)从B开始运动到A、B发生碰撞的时间内,木板C运动的位移为l-$\frac{{{v}_{0}}^{2}}{4μg}$.
点评 本题考查了动能定理的综合运用,运用动能定理解题,关键选择好研究的过程,分析过程中有哪些力做功,然后列式求解,难度中等.

 轻松暑假总复习系列答案
轻松暑假总复习系列答案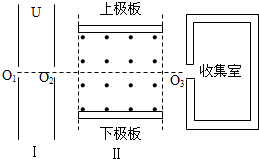 如图所示,一束带电粒子(不计重力,初速度可忽略)缓慢通过小孔O1进入极板间电压为U的水平加速电场区域Ⅰ,再通过小孔O2射入相互正交的恒定匀强电场、磁场区域Ⅱ,其中磁场的方向如图,磁感应强度大小可根据实际要求调节,收集室的小孔O3与O1、O2在同一条水平线上( )
如图所示,一束带电粒子(不计重力,初速度可忽略)缓慢通过小孔O1进入极板间电压为U的水平加速电场区域Ⅰ,再通过小孔O2射入相互正交的恒定匀强电场、磁场区域Ⅱ,其中磁场的方向如图,磁感应强度大小可根据实际要求调节,收集室的小孔O3与O1、O2在同一条水平线上( )| A. | 区域Ⅱ的电场方向竖直向下 | |
| B. | 该装置可筛选出具有特定质量的粒子 | |
| C. | 该装置可筛选出具有特定速度的粒子 | |
| D. | 若射入的粒子电荷量相同,则该装置筛选出的粒子一定具有相同的质量 |
| A. | 物体将继续在原来的圆周上运动 | |
| B. | 物体将沿着圆周的切线方向飞出去 | |
| C. | 物体将沿着切线和圆周之间的某一条曲线向远离圆心的方向运动 | |
| D. | 物体将朝着圆心运动 |
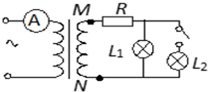 如图所示,理想变压器的副线圈上通过输电线接有两个相同的灯泡L1和L2,输电线的等效电阻为R,开始时,开关断开.当开关接通时,以下说法正确的是( )
如图所示,理想变压器的副线圈上通过输电线接有两个相同的灯泡L1和L2,输电线的等效电阻为R,开始时,开关断开.当开关接通时,以下说法正确的是( )| A. | 副线圈两端MN输出电压增大 | B. | 通过灯泡L1的电流减小 | ||
| C. | 电流表的示数减小 | D. | 变压器的输入功率变小 |
 如图所示,交流发电机线圈的面积为0.05m2,共100匝.该线圈在磁感应强度为$\frac{\sqrt{2}}{π}$T的匀强磁场中,以10πrad/s的角速度匀速转动,电阻R1和R2的阻值均为50Ω,线圈的内阻忽略不计,若从图示位置开始计时,则( )
如图所示,交流发电机线圈的面积为0.05m2,共100匝.该线圈在磁感应强度为$\frac{\sqrt{2}}{π}$T的匀强磁场中,以10πrad/s的角速度匀速转动,电阻R1和R2的阻值均为50Ω,线圈的内阻忽略不计,若从图示位置开始计时,则( )| A. | 线圈中的电动势为e=50$\sqrt{2}$sin10πtV | B. | 电流表的示数为1A | ||
| C. | 电压表的示数为25V | D. | R1上消耗的电功率为50W |
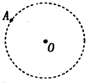 如图所示,A为太阳系中的天王星,它绕太阳O运行的轨道视为圆时,运动的轨道半径为R0,周期为T0.长期观测发现,天王星实际运动的轨道与圆轨道总有一些偏离,且每隔t0时间发生一次最大偏离,即轨道半径出现一次最大.根据万有引力定律,天文学家预言形成这种现象的原因可能是天王星外侧还存在着一颗未知的行星(假设其运动轨道与A在同一平面内,且与A的绕行方向相同),它对天王星的万有引力引起天王星轨道的偏离,由此可推测未知行星的运动轨道半径是( )
如图所示,A为太阳系中的天王星,它绕太阳O运行的轨道视为圆时,运动的轨道半径为R0,周期为T0.长期观测发现,天王星实际运动的轨道与圆轨道总有一些偏离,且每隔t0时间发生一次最大偏离,即轨道半径出现一次最大.根据万有引力定律,天文学家预言形成这种现象的原因可能是天王星外侧还存在着一颗未知的行星(假设其运动轨道与A在同一平面内,且与A的绕行方向相同),它对天王星的万有引力引起天王星轨道的偏离,由此可推测未知行星的运动轨道半径是( )| A. | $\frac{{t}_{0}}{{t}_{0}-{T}_{0}}$R0 | B. | R0$\sqrt{(\frac{{t}_{0}}{{t}_{0}-{T}_{0}})^{3}}$ | C. | R0$\root{3}{(\frac{{t}_{0}-{T}_{0}}{{t}_{0}})^{2}}$ | D. | R0$\root{3}{(\frac{{t}_{0}}{{t}_{0}-{T}_{0}})^{2}}$ |
| A. | 2倍 | B. | 4倍 | C. | 6 倍 | D. | 8倍 |
 近年来,智能手机的普及使“低头族”应运而生.近日研究发现,玩手机时,就有可能让颈椎承受多达60磅(约270N)的重量,相当于给颈椎挂俩大西瓜,比一个7岁小孩还重.不当的姿势与一系列健康问题存在关联,如背痛,体重增加、胃痛、偏头痛的呼吸道疾病等.当人体直立时,颈椎所承受的压力等于头部的重量;但当低头时,颈椎受到的压力会随之变化.现将人体头颈部简化为如图的模型;重心在P点的头部,在可绕O转动的颈椎OP(轻杆)的支持力和沿PQ方向肌肉拉力的作用下处于静止.当低头时,颈椎与竖直方向的夹角为45°,PQ与竖直方向的夹角为60°,此时,颈椎受到的压力约为直立时颈椎受到压力的( )
近年来,智能手机的普及使“低头族”应运而生.近日研究发现,玩手机时,就有可能让颈椎承受多达60磅(约270N)的重量,相当于给颈椎挂俩大西瓜,比一个7岁小孩还重.不当的姿势与一系列健康问题存在关联,如背痛,体重增加、胃痛、偏头痛的呼吸道疾病等.当人体直立时,颈椎所承受的压力等于头部的重量;但当低头时,颈椎受到的压力会随之变化.现将人体头颈部简化为如图的模型;重心在P点的头部,在可绕O转动的颈椎OP(轻杆)的支持力和沿PQ方向肌肉拉力的作用下处于静止.当低头时,颈椎与竖直方向的夹角为45°,PQ与竖直方向的夹角为60°,此时,颈椎受到的压力约为直立时颈椎受到压力的( )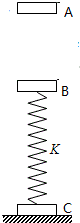 如图所示,物体A、B、C的质量均为1kg,其中B、C分别与轻质弹簧的两端连接在一起,将它们静置在地面上,现让A从B正上方5m高处又静止下落,A与B相碰,碰撞时间极短.相碰后两者立即粘在一起向下运动,以后不再分开.当A与B运动到最高点时,弹簧刚好恢复到原长,不计空气阻力,弹簧始终处于弹性限度内,弹簧劲度系数k=6N/m,重力加速度取10m/s2.
如图所示,物体A、B、C的质量均为1kg,其中B、C分别与轻质弹簧的两端连接在一起,将它们静置在地面上,现让A从B正上方5m高处又静止下落,A与B相碰,碰撞时间极短.相碰后两者立即粘在一起向下运动,以后不再分开.当A与B运动到最高点时,弹簧刚好恢复到原长,不计空气阻力,弹簧始终处于弹性限度内,弹簧劲度系数k=6N/m,重力加速度取10m/s2.