题目内容
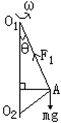
一小球质量为m,用长为L的悬绳(不可伸长,质量不计)固定于O点,在O点正下方 处钉有一颗钉子,如图所示,将悬线沿水平方向拉直无初速度释放后,当悬线碰到钉子后的瞬间:
处钉有一颗钉子,如图所示,将悬线沿水平方向拉直无初速度释放后,当悬线碰到钉子后的瞬间:

 处钉有一颗钉子,如图所示,将悬线沿水平方向拉直无初速度释放后,当悬线碰到钉子后的瞬间:
处钉有一颗钉子,如图所示,将悬线沿水平方向拉直无初速度释放后,当悬线碰到钉子后的瞬间:
| A.小球的线速度没有变化 |
| B.小球的角速度没有变化 |
| C.小球的向心加速度突然增大到原来的2倍 |
| D.悬线对小球的拉力突然增大到原来的2倍 |
AC
分析:小球在下摆过程中,受到线的拉力与小球的重力,由于拉力始终与速度方向相垂直,所以它对小球不做功,只有重力在做功.当碰到钉子瞬间,速度大小不变,而摆长变化,从而导致向心加速度变化,拉力变化.
解答:解:A、当碰到钉子瞬间,小球到达最低点时线速度没有变化,故A正确.
B、根据圆周运动知识得:ω=
 ,而半径变为原来的
,而半径变为原来的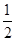 ,线速度没有变化,所以小球的角速度突然增大到原来的2倍,故B正确.
,线速度没有变化,所以小球的角速度突然增大到原来的2倍,故B正确.C、根据圆周运动知识得:a=
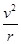 ,而半径变为原来的
,而半径变为原来的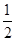 ,线速度没有变化,所以向心加速度突然增大到原来的2倍,故C正确;
,线速度没有变化,所以向心加速度突然增大到原来的2倍,故C正确;D、小球摆下后由机械能守恒可知,mgL=
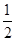 mv2,
mv2,因小球下降的高度相同,故小球到达最低点时的速度相同,v=

在最低点根据牛顿第二定律得:F-mg=ma=m
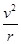 ,
,原来:r=L,F=mg+m
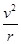 =3mg
=3mg而现在半径变为原来的
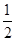 ,线速度没有变化.
,线速度没有变化.所以F′=mg+m
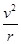 =5mg
=5mg悬线对小球的拉力突然增大到原来的
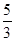 倍,故D错误
倍,故D错误故选AC.
点评:本题中要注意细绳碰到钉子前后转动半径的变化,再由向心力公式分析绳子上的拉力变化.小球摆到最低点虽与钉子相碰,但没有能量的损失.

练习册系列答案
 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案
相关题目
 向右做匀速运动,当小车遇到固定在地面的障碍物后,与之碰撞,碰后小车速度为零,关于碰后的运动(小车始终没有离开地面),下列说法正确的是( )
向右做匀速运动,当小车遇到固定在地面的障碍物后,与之碰撞,碰后小车速度为零,关于碰后的运动(小车始终没有离开地面),下列说法正确的是( )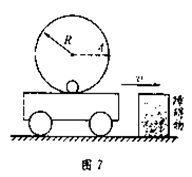





 通过转弯半径为
通过转弯半径为 的弯道时,内、外轨道均不受侧压力作用,下面分析正确的是
的弯道时,内、外轨道均不受侧压力作用,下面分析正确的是

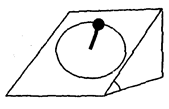
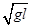 。( )
。( )
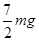
 ,质
,质 