题目内容
如图所示，不计滑轮质量与摩擦，重物挂在滑轮下，绳A端固定，将绳B端由B移到C或D（绳长不变）其绳上张力分别为TB，TC，TD，夹角θ分别为θB，θC，θD则（ ）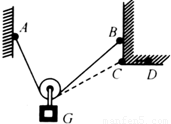
A．TB＞TC＞TD θB＜θC＜θD
B．TB＜TC＜TD θB＜θC＜θD
C．TB=TC＜TD θB=θC＜θD
D．TB=TC=TDθB=θC=θD
【答案】分析：先根据数学知识，得出滑轮两侧的绳子与竖直方向的夹角与A、B间距离和绳长的关系，分析此夹角是否变化，再对滑轮研究．根据平衡条件分析绳子张力和夹角如何变化．
解答：
解：设A与B（C）间的水平距离为S，绳子长度为L．由于滑轮上张力处处大小相等，则平衡时，滑轮两侧绳子关于竖直方向对称．
当绳B端由B移到C的过程中，设绳子与竖直方向的夹角为α，则由数学知识得
S=L1sinα+L2sinα=Lsinα
得 sinα=
，在此过程中，S、L均不变，则α不变，两绳之间的夹角θ=2α，可见，θ也不变，即有θB=θC．
根据滑轮平衡得知，两绳的张力大小也不变，即有TB=TC．
当绳B端由C移到D过程中，用同样的方法可知，sinα=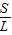
，S增大，L不变，α增大，两绳之间的夹角θ增大，则有θC＜θD．
根据平衡条件得：2Tcos
=G，当θ增大时，
增大，cos
减小，则知T增大，即有 TC＜TD．故C正确．
故选C
点评：本题结合有关滑轮的知识考查了三力作用下的物体平衡，物体的平衡是整个力学的难点，在平时训练中要加强这方面的练习．
解答：
解：设A与B（C）间的水平距离为S，绳子长度为L．由于滑轮上张力处处大小相等，则平衡时，滑轮两侧绳子关于竖直方向对称．当绳B端由B移到C的过程中，设绳子与竖直方向的夹角为α，则由数学知识得
S=L1sinα+L2sinα=Lsinα
得 sinα=
，在此过程中，S、L均不变，则α不变，两绳之间的夹角θ=2α，可见，θ也不变，即有θB=θC．根据滑轮平衡得知，两绳的张力大小也不变，即有TB=TC．
当绳B端由C移到D过程中，用同样的方法可知，sinα=
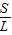，S增大，L不变，α增大，两绳之间的夹角θ增大，则有θC＜θD．根据平衡条件得：2Tcos
=G，当θ增大时，增大，cos减小，则知T增大，即有 TC＜TD．故C正确．故选C
点评：本题结合有关滑轮的知识考查了三力作用下的物体平衡，物体的平衡是整个力学的难点，在平时训练中要加强这方面的练习．
练习册系列答案
新课标阶梯阅读训练系列答案
相关题目
（2010?镇江一模）如图所示，长方体物块C置于水平地面上，物块A、B用不可伸长的轻质细绳通过滑轮连接（不计滑轮与绳之间的摩擦），A物块与C物块光滑接触，整个系统中的A、B、C三物块在水平恒定推力F作用下从静止开始以相同的加速度一起向左运动．下列说法正确的是（ ）
如图所示，绳的一端固定在墙上A点，另一端通过定滑轮吊一重物，杆BC可绕B点自由转动．杆、滑轮、绳质及摩擦均不计．将绳的A端沿墙稍向下移动，则下列判断中正确的是（ ）
如图所示，一条轻质细绳一端与A物体相连，另一端穿过C物体上的小孔后与B物体相连．它们的质量分别为mA=0.8kg．mB=mC=0.1kg，当B与C从静止开始下降h1=0.5m后，C被搁在平台上，B继续下降h2=0.3m后停止，求A与桌面之间的动摩因数多大？（不计滑轮及C小孔的摩擦）
