题目内容
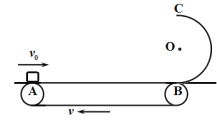
【题目】如图所示，水平的传送带长度L=8m，右端与半径R=0.5m的竖直光滑半圆轨道相连，圆轨道与传送带的末端B点相切，传送带在电机的驱动下以v=4m/s的速率顺时针匀速转动。一个质量m=2kg的物块（可以看成质点），以v0=2m/s的初速度从左端A点滑上传送带，物块与传送带间的动摩擦因数=0.2，重力加速g=10m/s2。求：
（1）物块从A运动到B的过程中，摩擦生热是多少？
（2）物块在圆轨道上运动时物块脱离圆轨道的点距离传送带平面多高？
【答案】（1）
（2）
【解析】（1）物块在传送带上加速运动过程中有：
由牛顿第二定律得： 
当物块速度等于传送带的速度时有： 
在0～t1的时间内，物块、皮带运动的路程S1，S2、分别为：
代入数据解得： 
，
所以物块与传送带共速之后匀速运动，不再打滑，因此物块在传送带上运动过程中摩擦生热为： 
（2）物块运动到B速度等于传送带的速度v，设物块在圆周的D点脱离，OD与水平的夹角为θ，在D点的速度为vD。因为在D点脱离，所以物块在D点轨道的作用力为： 
在D点由牛顿定律得： 
从B到D点，由动能定理得： 
D点到传送带平面的高度为： 
综上所述本题答案是：（1）
（2）
练习册系列答案
轻松夺冠全能掌控卷系列答案
相关题目
