题目内容
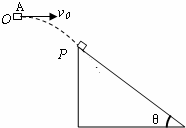
 如图所示,物块A(可视为质点)从O点水平抛出,抛出后经0.6s抵达斜面上端P处时速度方向与斜面平行.此后物块紧贴斜面向下运动,又经过2s物块到达斜面底端时的速度为14m/s.已知固定斜面的倾角θ=37°(且sin37°=0.6,cos37°=0.8),g取10m/s2.试求:
如图所示,物块A(可视为质点)从O点水平抛出,抛出后经0.6s抵达斜面上端P处时速度方向与斜面平行.此后物块紧贴斜面向下运动,又经过2s物块到达斜面底端时的速度为14m/s.已知固定斜面的倾角θ=37°(且sin37°=0.6,cos37°=0.8),g取10m/s2.试求:(1)抛出点O与P点的竖直距离h;
(2)物块A从O点水平抛出的初速度v0;
(3)物块与斜面之间的动摩擦因数μ.
分析:(1)物块A从O点水平抛出做平抛运动,由时间求出高度;
(2)根据平抛平抛时间0.6s,求出物A竖直方向的分速度,根据速度的分解求出物块A从O点水平抛出的初速度v0;
(3)由速度合成求出物块在P点的速度,结合经过2s物块到达斜面底端时的速度为14m/s,求出加速度,根据牛顿第二定律求出动摩擦因数μ.
(2)根据平抛平抛时间0.6s,求出物A竖直方向的分速度,根据速度的分解求出物块A从O点水平抛出的初速度v0;
(3)由速度合成求出物块在P点的速度,结合经过2s物块到达斜面底端时的速度为14m/s,求出加速度,根据牛顿第二定律求出动摩擦因数μ.
解答:解:(1)物块A从O点水平抛出做平抛运动,竖直方向做自由落体运动,则h=
gt2=
×10×0.62=1.8m
(2)0.6s时物A竖直方向的分速度vy=gt=6m/s
因为,
=tan37°
所以,v0=8m/s
(3)物块在P点的速度为v=
=10m/s 又a=
=2m/s2
根据牛顿第二定律得mgsinθ-f=ma
f=μN
代入得a=gsinθ-μgcosθ
联立上式可得:μ=0.5
答:(1)抛出点O与P点的竖直距离h=1.8m;
(2)物块A从O点水平抛出的初速度v0=8m/s;
(3)物块与斜面之间的动摩擦因数μ=0.5.
| 1 |
| 2 |
| 1 |
| 2 |
(2)0.6s时物A竖直方向的分速度vy=gt=6m/s
因为,
| vy |
| v0 |
所以,v0=8m/s
(3)物块在P点的速度为v=
|
| △v |
| △t |
根据牛顿第二定律得mgsinθ-f=ma
f=μN
代入得a=gsinθ-μgcosθ
联立上式可得:μ=0.5
答:(1)抛出点O与P点的竖直距离h=1.8m;
(2)物块A从O点水平抛出的初速度v0=8m/s;
(3)物块与斜面之间的动摩擦因数μ=0.5.
点评:本题是平抛运动和匀加速运动的综合,关键抓住两个过程的联系:平抛的末速度等于匀加速运动的初速度.

练习册系列答案
相关题目
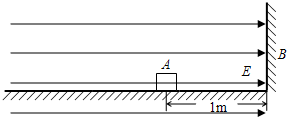 如图所示,物块A(可视为质点)的质量为1.0×10-2kg,带1.0×10-8C的正电荷.A与水平桌面间的动摩擦因数为μ=0.2,B为竖直挡板,A与挡板相距1.0m.A以6m/s的速度向B运动,在A运动的空间里存在着水平向右的匀强电场,场强E=8.0×106N/C.设A与B相碰无机械能损失,A在运动中电量不变.求物块A从图示位置开始到最后停止的过程中
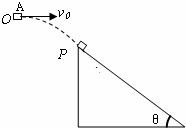
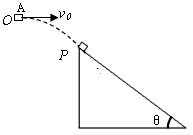
如图所示,物块A(可视为质点)的质量为1.0×10-2kg,带1.0×10-8C的正电荷.A与水平桌面间的动摩擦因数为μ=0.2,B为竖直挡板,A与挡板相距1.0m.A以6m/s的速度向B运动,在A运动的空间里存在着水平向右的匀强电场,场强E=8.0×106N/C.设A与B相碰无机械能损失,A在运动中电量不变.求物块A从图示位置开始到最后停止的过程中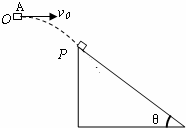 如图所示,物块A(可视为质点)从O点水平抛出,抛出后经0.6s抵达斜面上端P处时速度方向与斜面平行.此后物块紧贴斜面向下运动,又经过2s物块到达斜面底端时的速度为14m/s.已知固定斜面的倾角θ=37°(且sin37°=0.6,cos37°=0.8),g取10m/s2.试求:
如图所示,物块A(可视为质点)从O点水平抛出,抛出后经0.6s抵达斜面上端P处时速度方向与斜面平行.此后物块紧贴斜面向下运动,又经过2s物块到达斜面底端时的速度为14m/s.已知固定斜面的倾角θ=37°(且sin37°=0.6,cos37°=0.8),g取10m/s2.试求: