题目内容
14.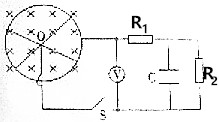 如图所示,一圆环由四根长度为L,电阻均为R的相互垂直的辐射条构成,现将圆环置于磁感应强度为B,方向垂直纸面向里的匀强磁场中,圆环以角速度ω绕O点逆时针转动,右侧电路(R1=$\frac{R}{4}$,R2=R,电容器电容为C),通过电刷与圆环中心和环缘相接触,S处于闭合状态,不计其他电阻以及一切摩擦,则下列判断正确的是( )
如图所示,一圆环由四根长度为L,电阻均为R的相互垂直的辐射条构成,现将圆环置于磁感应强度为B,方向垂直纸面向里的匀强磁场中,圆环以角速度ω绕O点逆时针转动,右侧电路(R1=$\frac{R}{4}$,R2=R,电容器电容为C),通过电刷与圆环中心和环缘相接触,S处于闭合状态,不计其他电阻以及一切摩擦,则下列判断正确的是( )| A. | 理想电压报示数为2BωL2 | B. | 流过R2的电流方向自下向上 | ||
| C. | 流过R2的电流强度大小为$\frac{2Bω{L}^{2}}{3R}$ | D. | 断开S,流过R2的电量为$\frac{Bω{L}^{2}C}{3}$ |
分析 辐条转动时会产生感应电动势,电压表测量路端电压.由右手定则判断感应电流的方向.由欧姆定律求出流过R2的电流强度.求出电容器的电压,得到电容器的带电量,即可得到断开S时流过R2的电量.
解答 解:A、辐条产生的感应电动势为 E=$\frac{1}{2}B{L}^{2}$ω,四根辐条的并联电阻为 r=$\frac{1}{4}$R
则理想电压表示数为 U=$\frac{{R}_{1}+{R}_{2}}{{R}_{1}+{R}_{2}+r}$E=$\frac{\frac{R}{4}+R}{\frac{R}{4}+R+\frac{R}{4}}$•$\frac{1}{2}B{L}^{2}$ω=$\frac{5}{12}B{L}^{2}$ω,故A错误.
B、由右手定则判断知,流过R2的电流方向自下向上,故B正确.
C、流过R2的电流强度大小 I=$\frac{E}{{R}_{1}+{R}_{2}+r}$=$\frac{B{L}^{2}ω}{3R}$,故C错误.
D、电容器的电压 UC=IR2=$\frac{1}{3}B{L}^{2}$ω,带电量为 Q=CUC=$\frac{1}{3}B{L}^{2}$ωC,故断开S,流过R2的电量为Q=$\frac{1}{3}B{L}^{2}$ωC.故D正确.
故选:BD
点评 本题是电磁感应中电路问题,关键要掌握转动切割的感应电动势公式E=$\frac{1}{2}B{L}^{2}$ω及欧姆定律等等基本知识,知道电压表测量外电压.

练习册系列答案
相关题目
4.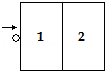 如图所示,一冰壶做匀减速直线运动,以速度v垂直进入第一个矩形区域的左边,刚要离开第二个矩形区域时速度恰好为零,则冰壶依次进入每个矩形区域时的速度之比和穿过每个矩形区域所用的时间之比分别是(设冰壶可看成质点,两个矩形区域宽度相同)( )
如图所示,一冰壶做匀减速直线运动,以速度v垂直进入第一个矩形区域的左边,刚要离开第二个矩形区域时速度恰好为零,则冰壶依次进入每个矩形区域时的速度之比和穿过每个矩形区域所用的时间之比分别是(设冰壶可看成质点,两个矩形区域宽度相同)( )
 如图所示,一冰壶做匀减速直线运动,以速度v垂直进入第一个矩形区域的左边,刚要离开第二个矩形区域时速度恰好为零,则冰壶依次进入每个矩形区域时的速度之比和穿过每个矩形区域所用的时间之比分别是(设冰壶可看成质点,两个矩形区域宽度相同)( )
如图所示,一冰壶做匀减速直线运动,以速度v垂直进入第一个矩形区域的左边,刚要离开第二个矩形区域时速度恰好为零,则冰壶依次进入每个矩形区域时的速度之比和穿过每个矩形区域所用的时间之比分别是(设冰壶可看成质点,两个矩形区域宽度相同)( )| A. | v1:v2=2:1 | B. | v1:v2=$\sqrt{2}$:1 | C. | t1:t2=1:$\sqrt{2}$ | D. | t1:t2=($\sqrt{2}$-1):1 |
9. 如图,斜面上a、b、c三点等距,小球从a点正上方抛出,做初速为v0的平抛运动,恰落在b点.若小球抛出点不变,初速变为v,其落点位于c,则( )
如图,斜面上a、b、c三点等距,小球从a点正上方抛出,做初速为v0的平抛运动,恰落在b点.若小球抛出点不变,初速变为v,其落点位于c,则( )
 如图,斜面上a、b、c三点等距,小球从a点正上方抛出,做初速为v0的平抛运动,恰落在b点.若小球抛出点不变,初速变为v,其落点位于c,则( )
如图,斜面上a、b、c三点等距,小球从a点正上方抛出,做初速为v0的平抛运动,恰落在b点.若小球抛出点不变,初速变为v,其落点位于c,则( )| A. | v=2v0 | B. | v>2v0 | C. | v<2v0 | D. | 2v0<v<3v0 |
19. 如图所示,一根匀质绳的质量为M,其两端固定在天花板上的A、B两点.在绳的中点悬挂一质量为m的重物,悬挂重物的绳质量不计,设α、β分别为绳的端点和中点处的切线方向与竖直方向的夹角,则$\frac{tanα}{tanβ}$的大小为( )
如图所示,一根匀质绳的质量为M,其两端固定在天花板上的A、B两点.在绳的中点悬挂一质量为m的重物,悬挂重物的绳质量不计,设α、β分别为绳的端点和中点处的切线方向与竖直方向的夹角,则$\frac{tanα}{tanβ}$的大小为( )
 如图所示,一根匀质绳的质量为M,其两端固定在天花板上的A、B两点.在绳的中点悬挂一质量为m的重物,悬挂重物的绳质量不计,设α、β分别为绳的端点和中点处的切线方向与竖直方向的夹角,则$\frac{tanα}{tanβ}$的大小为( )
如图所示,一根匀质绳的质量为M,其两端固定在天花板上的A、B两点.在绳的中点悬挂一质量为m的重物,悬挂重物的绳质量不计,设α、β分别为绳的端点和中点处的切线方向与竖直方向的夹角,则$\frac{tanα}{tanβ}$的大小为( )| A. | $\frac{tanα}{tanβ}$=$\frac{M+m}{m}$ | B. | $\frac{tanα}{tanβ}$=$\frac{M}{m}$ | C. | $\frac{tanα}{tanβ}$=$\frac{m}{m+M}$ | D. | $\frac{tanα}{tanβ}$=$\frac{m}{M}$ |
20.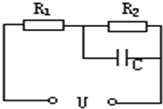 如图的电路中,U=8V不变,电容器电容C=200μF,R1:R2=5:3,则R2两端的电压U2与电容器的带电量Q分别为为( )
如图的电路中,U=8V不变,电容器电容C=200μF,R1:R2=5:3,则R2两端的电压U2与电容器的带电量Q分别为为( )
 如图的电路中,U=8V不变,电容器电容C=200μF,R1:R2=5:3,则R2两端的电压U2与电容器的带电量Q分别为为( )
如图的电路中,U=8V不变,电容器电容C=200μF,R1:R2=5:3,则R2两端的电压U2与电容器的带电量Q分别为为( )| A. | U2=8V,Q=1.6×10-3C | B. | U2=3V,Q=6×10-4C | ||
| C. | U2=5V,Q=1×10-3C | D. | U2=4V,Q=8×10-4C |
 如图所示,电源电动势为3V,内阻为0.5Ω,电路中的电阻R1=R2=2Ω,R4=R5=4Ω,R3=3Ω,电流表、电压表均为理想电表.求:
如图所示,电源电动势为3V,内阻为0.5Ω,电路中的电阻R1=R2=2Ω,R4=R5=4Ω,R3=3Ω,电流表、电压表均为理想电表.求: 如图所示的电路中,电源电动势E=3V,内电阻r=1Ω,定值电阻R1=2Ω,R2=3Ω,电容器的电容C=100μF,闭合开关s,电路稳定后电容器极板b的带电量为1.5×10-4C.先闭合开关s,电路稳定后断开开关s,通过电阻R2的电量为1.5×10-4C.
如图所示的电路中,电源电动势E=3V,内电阻r=1Ω,定值电阻R1=2Ω,R2=3Ω,电容器的电容C=100μF,闭合开关s,电路稳定后电容器极板b的带电量为1.5×10-4C.先闭合开关s,电路稳定后断开开关s,通过电阻R2的电量为1.5×10-4C. 如图所示,一小球以初速度v0水平抛出,落地速度为v,不计空气阻力,求小球在此期间位移的大小.
如图所示,一小球以初速度v0水平抛出,落地速度为v,不计空气阻力,求小球在此期间位移的大小. 如图所示,木板静止于水平地面上,在其最右端放一可视为质点的木块.已知木块的质量m=1kg,木板的质量M=4kg,长L=2.5m,上表面光滑,下表面与地面之间的动摩擦因数μ=0.2.现用水平恒力F=20N拉木板,g取10m/s2,求:
如图所示,木板静止于水平地面上,在其最右端放一可视为质点的木块.已知木块的质量m=1kg,木板的质量M=4kg,长L=2.5m,上表面光滑,下表面与地面之间的动摩擦因数μ=0.2.现用水平恒力F=20N拉木板,g取10m/s2,求: