题目内容
7.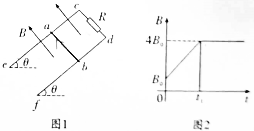 如图1所示,由足够长的平行金属轨道ce、df确定的平面与水平面间的夹角为θ=60°,c、d端接有阻值为R的电阻,导体棒ab垂直于轨道放置在轨道上.轨道间距离为L,轨道间垂直于轨道平面向上的匀强磁场,磁感应强度B随时间t的变化规律如图2所示.0-t1时间内,棒ab静止在轨道上,且t1时刻恰好要沿轨道滑动,棒ab与cd端的距离为L.棒ab与两轨道接触良好,且其沿轨道下滑过程中始终与轨道垂直,轨道和棒的电阻不计,最大静摩擦力等于滑动摩擦力,求:
如图1所示,由足够长的平行金属轨道ce、df确定的平面与水平面间的夹角为θ=60°,c、d端接有阻值为R的电阻,导体棒ab垂直于轨道放置在轨道上.轨道间距离为L,轨道间垂直于轨道平面向上的匀强磁场,磁感应强度B随时间t的变化规律如图2所示.0-t1时间内,棒ab静止在轨道上,且t1时刻恰好要沿轨道滑动,棒ab与cd端的距离为L.棒ab与两轨道接触良好,且其沿轨道下滑过程中始终与轨道垂直,轨道和棒的电阻不计,最大静摩擦力等于滑动摩擦力,求:(1)棒ab与轨道间的动摩擦因数;
(2)电阻R上的最大电功率和棒获得的最大速度.
分析 (1)由法拉第电磁感应定律求出感应电动势,由欧姆定律求出电流,应用安培力公式求出安培力,然后应用平衡条件求出动摩擦因数.
(2)当导体棒匀速运动时导体棒的速度最大,应用安培力公式求出安培力,然后由平衡条件求出最大速度,应用电功率公式求出最大电功率.
解答 解:(1)由法拉第电磁感应定律可知,在0-t1内产生的感应电动势:
$\overline{E}$=$\frac{△Φ}{△t}$=$\frac{△B•S}{△t}$=$\frac{(4{B}_{0}-{B}_{0})×{L}^{2}}{{t}_{1}}$=$\frac{3{B}_{0}{L}^{2}}{{t}_{1}}$,
感应电流:$\overline{\;}$$\overline{I}$=$\frac{\overline{E}}{R}$=$\frac{3{B}_{0}{L}^{2}}{R{t}_{1}}$,
t1时刻,导体棒受到的安培力:F=BIL=4B0$\overline{I}$L=$\frac{12{B}_{0}^{2}{L}^{3}}{R{t}_{1}}$,
由平衡条件得:mgsin60°+μmgcos60°=$\frac{12{B}_{0}^{2}{L}^{3}}{R{t}_{1}}$,
解得,动摩擦因数:μ=$\frac{24{B}_{0}^{2}{L}^{3}}{R{t}_{1}mg}$-$\sqrt{3}$;
(2)导体棒匀速运动时速度最大,
安培力:F安培=BIL=4B0×$\frac{4{B}_{0}Lv}{R}$×L=$\frac{16{B}_{0}^{2}{L}^{2}v}{R}$,
导体棒匀速运动,由平衡条件得:
mgsin60°=$\frac{16{B}_{0}^{2}{L}^{2}v}{R}$+μmgcos60°,
解得,最大速度:v=$\frac{\sqrt{3}mgR}{16{B}_{0}^{2}{L}^{2}}$-$\frac{3L}{4{t}_{1}}$,
感应电动势:E=4B0Lv=$\frac{\sqrt{3}mgR}{4{B}_{0}L}$-$\frac{3{B}_{0}{L}^{2}}{{t}_{1}}$,
最大电功率:P=$\frac{{E}^{2}}{R}$=$\frac{1}{R}$($\frac{\sqrt{3}mgR}{4{B}_{0}L}$-$\frac{3{B}_{0}{L}^{2}}{{t}_{1}}$)2,
答:(1)棒ab与轨道间的动摩擦因数为$\frac{24{B}_{0}^{2}{L}^{3}}{R{t}_{1}mg}$-$\sqrt{3}$;
(2)电阻R上的最大电功率为:$\frac{1}{R}$($\frac{\sqrt{3}mgR}{4{B}_{0}L}$-$\frac{3{B}_{0}{L}^{2}}{{t}_{1}}$)2,棒获得的最大速度为$\frac{\sqrt{3}mgR}{16{B}_{0}^{2}{L}^{2}}$-$\frac{3L}{4{t}_{1}}$.
点评 本题考查了求动摩擦因数、速度与功率问题,对导体棒正确受力分析,应用平衡条件、E=BLv、电功率公式即可解题.

 一线名师权威作业本系列答案
一线名师权威作业本系列答案
| A. | v=50cm/s,向右传播 | B. | v=25cm/s,向左传播 | ||
| C. | v=50cm/s,向左传播 | D. | v=25cm/s,向右传播 |
| A. | 0.5m/s,9.0m/s | B. | 1.0m/s,9.5m/s | C. | 1.5m/s,95m/s | D. | 0.5m/s,9.5m/s |
 如图所示,某人用托里拆利管做测定大气压强的实验时,由于管内漏进了空气,测得管内汞柱的高度仅为70cm,但当时的实际大气压强为一个标准大气压(相当于76cm高的汞柱产生的压强).今采用下述哪种方法,可使管内、外汞面的高度差大于70cm( )
如图所示,某人用托里拆利管做测定大气压强的实验时,由于管内漏进了空气,测得管内汞柱的高度仅为70cm,但当时的实际大气压强为一个标准大气压(相当于76cm高的汞柱产生的压强).今采用下述哪种方法,可使管内、外汞面的高度差大于70cm( )| A. | 把托里拆利管逐渐倾斜(管子露出部分长度不变) | |
| B. | 把托里拆利管慢慢向上提,但下端不离开汞樔 | |
| C. | 保持装置不动,往汞槽内加汞,以增大压强 | |
| D. | 整个装置竖直向上做加速运动 |
| A. | 所有地球同步卫星一定在赤道上空 | |
| B. | 不同的地球同步卫星,离地高度不同 | |
| C. | 所有地球同步卫星的向心加速度大小和方向一定相同 | |
| D. | 所有地球同步卫星受的向心力大小一定相等 |
 如图,电源A的电压为6v,电源B的电压为8V,当电键K从A转到B时,通过电流计的电量为1.4×10-5C;则电容器的电容为( )
如图,电源A的电压为6v,电源B的电压为8V,当电键K从A转到B时,通过电流计的电量为1.4×10-5C;则电容器的电容为( )| A. | 2×10-5F | B. | 1.5×10-6F | C. | 6×10-6F | D. | 1×10-6F |
| A. | 物理学家库仑利用扭秤实验发现了电荷间的相互作用规律 | |
| B. | 物理学家法拉第通过油滴实验精确测定了元电荷e的电荷量 | |
| C. | 物理学家密立根最早引入了电场概念,并提出用电场线表示电场 | |
| D. | 物理学家卡文迪许测出了静电力常量k |
 如图所示,斜面轨道AB与水平面之间的夹角θ=53°,BD为半径R=4m的圆弧形轨道,且B点与D点在同一水平面上,在B点,斜面轨道AB与圆弧形轨道BD相切,整个轨道处于竖直平面内且处处光滑,在A点处有一质量m=1kg的小球由静止滑下,经过B、C两点后从D点斜抛出去,最后落在地面上的S点时的速度大小vS=8m/s,已知A点距地面的高度H=10m,B点距地面的高度h=5m,设以MDN为分界线,其左边为一阻力场区域,右边为真空区域,g取10m/s2,cos53°=0.6,求:
如图所示,斜面轨道AB与水平面之间的夹角θ=53°,BD为半径R=4m的圆弧形轨道,且B点与D点在同一水平面上,在B点,斜面轨道AB与圆弧形轨道BD相切,整个轨道处于竖直平面内且处处光滑,在A点处有一质量m=1kg的小球由静止滑下,经过B、C两点后从D点斜抛出去,最后落在地面上的S点时的速度大小vS=8m/s,已知A点距地面的高度H=10m,B点距地面的高度h=5m,设以MDN为分界线,其左边为一阻力场区域,右边为真空区域,g取10m/s2,cos53°=0.6,求: