题目内容
用两根绳子吊起一个重物，如图所示，如果AO、BO绳所能承受的最大拉力均是2.0×104N，（sin37°=0.6，sin53°=0.8）求：
（1）吊起重物重力逐渐增大时，AO段和BO段哪根绳先断？（请作图判断，不须文字说明．）
（2）该装置所能吊起的重物最重是多少？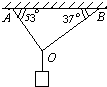
（1）吊起重物重力逐渐增大时，AO段和BO段哪根绳先断？（请作图判断，不须文字说明．）
（2）该装置所能吊起的重物最重是多少？
（1）假设两绳均不被拉断．分析O点受力情况，作出力图，如图．由图看出，TBO＜TAO，说明绳子AO的拉力先达到最大值，则知AO绳先断．
（2）由上知，当AO绳的拉力达到最大时此时所吊起的重物最重，最大重力为
G=
=
N=2.5×104N
答：（1）吊起重物重力逐渐增大时，AO段绳先断．（2）该装置所能吊起的重物最重是2.5×104N．
（2）由上知，当AO绳的拉力达到最大时此时所吊起的重物最重，最大重力为
G=
| TAO |
| sin53° |
| 2.0×104 |
| 0.8 |
答：（1）吊起重物重力逐渐增大时，AO段绳先断．（2）该装置所能吊起的重物最重是2.5×104N．
练习册系列答案
培优三好生系列答案
相关题目
用两根绳子吊起一个重物，如图所示，如果AO、BO绳所能承受的最大拉力均是2.0×104N，（sin37°=0.6，sin53°=0.8）求：
用两根绳子吊起一个重物，如图所示．如果AO和BO两根绳所能承受的最大拉力都是200N，求：（sin37°=0.6，sin53°=cos37°=0.8 ）
用两根绳子吊起一个重物，如图10所示，如果每根绳所能承受的最大拉力是2.0
104N（sin37?＝0.6，sin53?＝0.8）求：
104N，（sin37º＝0.6，sin53º＝0.8）则：
104N，（sin37º＝0.6，sin53º＝0.8）则：