题目内容
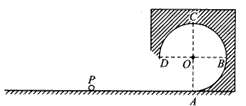
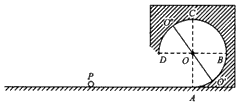
匀强电场水平向右，电场强度为E，水平轨道和竖直圆形轨道相切于圆形轨道的最低端A，轨道均绝缘光滑。圆形轨道的半径为R一个质量为m所带电荷量为q的小球由P点静止释放。
（1）要让小球刚好能到达和圆心在同一高度的B点，求PA的水平距离？
（2）要让小球刚好能到达轨道的最高点C，求PA的水平距离？
（3）要让小球刚好能做完整的圆周运动，求PA的水平距离？
（1）要让小球刚好能到达和圆心在同一高度的B点，求PA的水平距离？
（2）要让小球刚好能到达轨道的最高点C，求PA的水平距离？
（3）要让小球刚好能做完整的圆周运动，求PA的水平距离？
解：设小球速度为零时可静止在轨道上的O'点，OO'与竖直方向的夹角为θ，tanθ=Eq/mg，此处相当于物理上的最低点
（1）因OB和OO'的夹角小于90°，所以小球到达B点的速度可以为零
由动能定理可得Eq（PA+R）－mgR=0－0
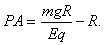
（2）因OC和OO'的夹角大于90°，所以小球到达B点速度不为零
重力充当向心力，mg=mv2/R，得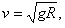
由动能定理可得EqPA－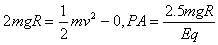
（3）图中C点只是地理上的最高点，将
等效成新的重力场，则O''就成为物理上的最高点，也是最难通过的点，所以只要小球能通过O'关于O的对应点O''就可以做完整的圆周运动
在O''点：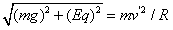
由动能定理可得从P点到O''点有：
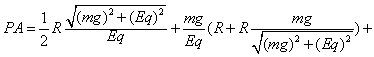
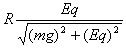
（1）因OB和OO'的夹角小于90°，所以小球到达B点的速度可以为零
由动能定理可得Eq（PA+R）－mgR=0－0
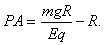
（2）因OC和OO'的夹角大于90°，所以小球到达B点速度不为零
重力充当向心力，mg=mv2/R，得
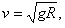
由动能定理可得EqPA－
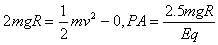
（3）图中C点只是地理上的最高点，将
等效成新的重力场，则O''就成为物理上的最高点，也是最难通过的点，所以只要小球能通过O'关于O的对应点O''就可以做完整的圆周运动在O''点：
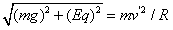
由动能定理可得从P点到O''点有：
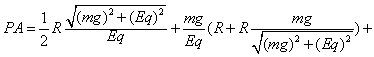
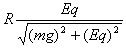
练习册系列答案
相关题目
如图所示竖直放置的光滑绝缘圆环穿有一带负电的小球，匀强电场水平向右，小球绕O点作圆周运动，那么（ ）
如图所示，匀强电场水平向右，虚线为两个带电粒子运动的轨迹，粒子只受电场力的作用，则以下判断正确的是（ ）
如图所示，竖直放置的光滑绝缘圆环穿有一带正电的小球，匀强电场水平向右，小球绕O点作圆周运动，那么以下错误的（ ）
（2009?徐州二模）如图所示，匀强电场水平向右，虚线右边空间存在着方向水平、垂直纸面向里的匀强磁场，虚线左边有一固定的光滑水平杆，杆右端恰好与虚线重合．有一电荷量为q、质量为m的小球套在杆上并从杆左端由静止释放，带电小球离开杆的右端进入正交电、磁场后，开始一小段时间内，小球（ ）
（2012?杭州模拟）如图所示，匀强电场水平向右，匀强磁场垂直纸面向里，带正电的小球在场中静止释放，最后落到地面上．关于该过程，下述说法正确的是（ ）